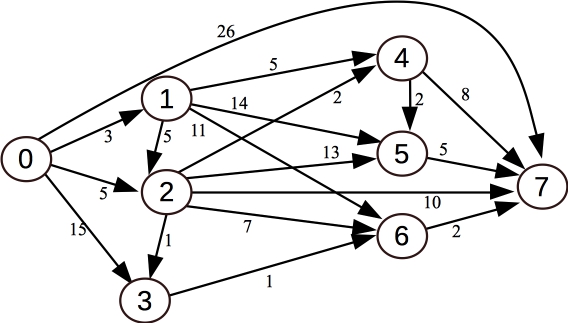CS302 Final Exam - Answers and Grading

James S. Plank - December 9, 2015

Question 1

In the problem specification, |V| = n, and unless otherwise specified, |E| = O(n²). For that reason, if an algorithm's running time is O(|V|+|E|), the answer will be O(n²). This is because O(n+n²) is in fact O(n²). Similarly, O(|E|log|V|) is O(n²log n).

A: Straight from the lecture notes: O(n). Class performance. 82%
B: This is DFS on a graph. Since the graph has one cycle, it has at most n edges: O(n). I gave 1.2 points (of two) for answering O(n²), if you incorrectly assumed that there would be O(n²) edges in this graph. Class performance: 50% correct, 30% answered O(n²).
C: Straight from the lecture notes: O(|V|+|E|) = O(n²). I gave 0.75 points for O(n) -- I'm assuming that those who answered that were thinking that connected components (DFS) is linear, and O(n) is "linear." Class performance: 33% correct. 41% answered O(n).
D: Straight from the lecture notes: O(n²). Class performance: 61% correct. 22% answered O(n log n), which is never the case with insertion sort.
E: Straight from the lecture notes: O(|E|log|V|) = O(n²log n). I gave 1 point to O(n log n), where I'm guessing that students equated O(|E|log|V|) with O(n log n). Class performance: 33% correct. 44% answered O(n log n).
F: Straight from the lecture notes: O(n log n). Class performance: 74% correct.
G: Once again, straight from the lecture notes: O(n). Class performance: 67 correct%
H: Straight from the lecture notes: O(|V|+|E|) = O(n²). I gave half credit to O(n) for the same reason as in C. Class performance: 22% correct. 48% answered O(n).
I: O(|E|log|E|) = O(n²log n²) = O(n²log n). As with E, I gave half credit to O(n log n). Class performance: 28% correct. 44% answered O(n log n).
J: After you have found the final residual graph, you perform a DFS to find all of the nodes reachable from the source in the original graph: O(|V|+|E|) = O(n²). As with part H, I gave half credit to O(n). Class performance: 30% correct. 31% answered O(n).
K: Straight from the lecture notes: Breadth-first search: O(|V|+|E|) = O(n²). I gave half credit again for O(n). Class performance: 35% correct. 33% answered O(n).
L: This involves doing a constant amount of work for every edge on the path. The path can have a maximum of n nodes, so this is O(n). I gave 0.7 points for O(n²), since that is the potential number of edges in the graph. However, a path can only have n-1 edges. Class performance: 57% correct. 13% answered O(n²).

Grading

Two points per part. I explain partial credit above.

Question 2

A: That is Prim's algorithm. Kruskal's algorithm starts by sorting the edges (or putting them into a heap), and then processing them in increasing order: False. Class performance: 82% correct.
B: The maximum flow is equal to the sum of the weights of the edges in the minimum cut. By definition, the minimum cut is a collection of edges, so this has to be True. Class performance: 83% correct.
C: It depends on the graph. This is the topic of the last half of the lecture on Topological Sort, where we show graphs for which Topological sort is faster, and graphs where Dijkstra's algorithm is faster: False. Class performance: 70% correct.
D: With merge sort, you need to have a second copy of the vector. You perform quicksort in place. This is false. Class performance: 94%.
E: This is very close to the example that I gave in the lecture notes on insertion sort. I generated a vector where each element is 10 places from its final resting place, and showed how insertion sort was linear on that vector. In this question, the running time will be 50 moves per element at maximum, which is O(n): True. Class performance: 52%.
F: It finds the best pivot from the three elements that it examines, but it doesn't find the best pivot overall. Think of it this way -- suppose the vector is { 1, 2, 3, 4, 5, 1, 6, 7, 8, 9, 10, 1 } The median of three is going to choose 1 as the pivot, which is clearly not the best: False. I understand though, that many of you read this question to be that it chooses the best of the three pivots. For that reason, I gave full credit to both True and False.
G: This is exactly what memoization does: True. Class performance: 96%.
H: They both may be done in place, and require the same amount of memory. This is False. This was the only question where the class performed under 50%. I'm guessing that most of you thought about implementing heapsort with a separate heap data structure, which does take more memory. Please see the lecture notes under heap sort. Class performance: 37%.
I: Bucket sort only works in linear time when you know the probability distribution of the input. In the example of the lecture notes, we leveraged the fact that we knew that the numbers were uniformly distributed between 0 and 1: False. Class performance: 54%.
J: Yes, that is exactly how we did it in the network flow lecture: True. Class performance: 93%.

Grading

Parts A, B, D, E, G and J were all worth two points, because in my opinion, they were straightfoward tests of things that were from the lecture notes. I deemed that the others were more difficult, so I only weighted them one point each.

Question 3

Part A: You can draw the graph if you want to see it. I'll draw it below if that helps you visualize the answer.

However, you can solve the problem just by knowing the adjacency list for node 2, because that is the next node that you will process from the multimap. That node has a shortest distance of 5 from node zero. So, let's process each node on node 2's adjacency list:

You can get to node 3 in 5+1 = 6 units. That is better than the current best distance to 3, which is 15. So, you'll delete the current [15,3] from the multimap and insert [6,3].
You can get to node 4 in 5+2 = 7 units. That is better than the current best distance to 4, which is 8. So, you'll delete the current [8,4] from the multimap and insert [7,4].
You can get to node 5 in 5+13 = 18 units. That doesn't improve 5's current distance of 17, so you will do nothing with node 5.
You can get to node 6 in 5+7 = 12 units. That is better than the current best distance to 6, which is 14. So, you'll delete the current [14,6] from the multimap and insert [12,6].
You can get to node 7 in 5+10 = 15 units. That is better than the current best distance to 7, which is 26. So, you'll delete the current [15,7] from the multimap and insert [15,7].

The final answer is: { [6,3] [7,4] [12,6] [15,7] [17,5] }. If you don't delete entries of the multimap when you replace them, then the answer is: { [6,3] [7,4] [8,4] [12,6] [14,6] [15,3] [15,7] [17,5] [26,7] }. Part B: We perform the same exercise, but with spanning tree rather than distance:

You can add 3 to the spanning tree with an edge whose weight is 1. That is better than the current smallest edge, which is 15. So, you'll delete the current [15,3] from the multimap and insert [1,3].
You can add 4 to the spanning tree with an edge whose weight is 2. That is better than the current smallest edge, which is 5. So, you'll delete the current [5,4] from the multimap and insert [2,4].
You can add 5 to the spanning tree with an edge whose weight is 13. That is better than the current smallest edge, which is 14. So, you'll delete the current [14,5] from the multimap and insert [13,5].
You can add 6 to the spanning tree with an edge whose weight is 7. That is better than the current smallest edge, which is 11. So, you'll delete the current [11,6] from the multimap and insert [7,6].
You can add 7 to the spanning tree with an edge whose weight is 10. That is better than the current smallest edge, which is 26. So, you'll delete the current [26,7] from the multimap and insert [10,7].

The final answer is: { [1,3] [2,4] [7,6] [10,7] [13,5] } If you don't delete entries of the multimap when you replace them, then the answer is: { [1,3] [2,4] [5,4] [7,6] [10,7] [11,6] [13,5] [14,5] [15,3] [26,7] }.

Grading

7 points per part. I gave some partial credit.

Question 4

This is very similar to the IncreasingSubsequences program that we went over in the lecture notes on Topological Sort. Start by setting the number of paths for node from to one, and all of ther numbers of paths to zero. Then perform a topological sort. Since node from is the only one with zero incident edges (this is because you can reach every other node from node from), that's the only one you have to push onto your deque. Then process the nodes using topological sort, adding a node's number of paths to each of the nodes adjacent to it. When you reach node to return its number of paths. Here is an answer:

(BTW, you don't need to use a deque. You can use a vector so long as you push and pop from the back).

long long Graph::Num_Paths(int from, int to)
{
  int i, n, t;
  deque <int> zero_inc;

  /* Set all paths to zero, except for node <b>from</b>, where there is one. */

  for (i = 0; i < Paths.size(); i++) Paths[i] = 0;
  Paths[from] = 1;

  /* You need a deque of nodes which have zero incident edges. 
     The only node on this deque when you start is node from. */

  zero_inc.push_back(from);

  /* Process the list. */

  while (!zero_inc.empty()) {

    /* Pull the first node off, and delete it */

    n = zero_inc[0];
    zero_inc.pop_front();

    /* If this is to, then we're done -- return the number of paths
       to to that is held in the vector Paths. */

    if (n == to) return Paths[to];

    /* Add the current node's number of paths to each node adjacent to it.
       Then "delete" the edge by decrementing that node's indicent edges.
       When that value hits zero, pust the node onto the deque. */

    for (i = 0; i < Adj[n].size(); i++) {
      t = Adj[n][i];
      Paths[t] += Paths[n];
      Incident[t]--;
      if (Incident[t] == 0) zero_inc.push_back(t); 
    }
  }
  return Paths[to];   /* This shouldn't happen because all nodes
                         are reachable from node "from" */
}

I've programmed this up in Graph.cpp, and put a main() that reads the number of nodes, and then the edges. Nodes are numbered from 0 to the number of nodes minus one. I've put examples 0 and 3 from the IncreasingSubsequences problems into the files. G1.txt and G2.txt. I've put a denser graph with 31 nodes into G3.txt. This program works well on all three files:

UNIX> g++ -o Graph Graph.cpp
UNIX> time ./Graph < G1.txt
4
0.000u 0.000s 0:00.00 0.0%	0+0k 0+0io 0pf+0w
UNIX> time ./Graph < G2.txt
41
0.001u 0.000s 0:00.00 0.0%	0+0k 0+0io 0pf+0w
UNIX> time ./Graph < G3.txt
531372800
0.001u 0.000s 0:00.00 0.0%	0+0k 0+0io 0pf+0w
UNIX>

Other Approaches, Working and Non-Working

Many of you didn't identify this problem as topological sort, and tried other approaches. I'll address these in turn:

DFS

You can structure this recursively, like a DFS -- call Num_Paths() on each of your children, and sum the return values. If you call Num_Paths(to, to), then return 1. I have this solution in Graph2.cpp. You'll note that it doesn't use Paths or Incident:

long long Graph::Num_Paths(int from, int to)
{
  long long rv;
  int i;

  if (from == to) return 1;
  
  rv = 0;
  for (i = 0; i < Adj[from].size(); i++) {
    rv += Num_Paths(Adj[from][i], to);
  }
  return rv;
}

It works on the first two files, but it takes 12 seconds on G3.txt, because it's not a true DFS -- it calls Num_Paths() on the same node multiple times, and these calls blow up exponentially in G3.txt:

UNIX> time ./Graph2 < G1.txt
4
0.000u 0.000s 0:00.00 0.0%	0+0k 0+0io 0pf+0w
UNIX> time ./Graph2 < G2.txt
41
0.001u 0.000s 0:00.00 0.0%	0+0k 0+0io 0pf+0w
UNIX> time ./Graph2 < G3.txt
531372800
12.551u 0.008s 0:12.56 99.9%	0+0k 0+0io 0pf+0w
UNIX>

Memoizing the DFS

You can memoize the DFS like it's a dynamic program -- now the running time is linear again (I'm using Paths as the cache, and setting all entries to -1 at the beginning of the program). This is in Graph3.cpp:

long long Graph::Num_Paths(int from, int to)
{
  long long rv;
  int i;

  if (from == to) return 1;
  if (Paths[from] != -1) return Paths[from];
  
  rv = 0;
  for (i = 0; i < Adj[from].size(); i++) {
    rv += Num_Paths(Adj[from][i], to);
  }
  Paths[from] = rv;
  return rv;
}

UNIX> g++ -o Graph3 Graph3.cpp
UNIX> time ./Graph3 < G1.txt
4
0.000u 0.001s 0:00.00 0.0%	0+0k 0+0io 0pf+0w
UNIX> time ./Graph3 < G2.txt
41
0.001u 0.000s 0:00.00 0.0%	0+0k 0+0io 0pf+0w
UNIX> time ./Graph3 < G3.txt
531372800
0.001u 0.001s 0:00.00 0.0%	0+0k 0+0io 0pf+0w
UNIX>

Using recursion to do the topological sort

This one is harder to get correct, but you can perform the topological sort using recursion -- when you set a node's Incidence to 0, you call Num_Paths recursively. This assumes that Paths is initialized to zero for every node. Compare this solution with the first solution above -- they are quite similar, but this one doesn't manage a deque or vector explicitly. The other solution is more straightfoward. This is in Graph4.cpp:

long long Graph::Num_Paths(int from, int to)
{
  long long rv;
  int tn;
  int i;

  if (from == to) return Paths[from];

  rv = 0;
  for (i = 0; i < Adj[from].size(); i++) {
    tn = Adj[from][i];
    Paths[tn] += Paths[from];
    Incident[tn]--;
    if (Incident[tn] == 0) rv = Num_Paths(tn, to);
  }
  return rv;
}

UNIX> g++ -o Graph4 Graph4.cpp
UNIX> time ./Graph4 < G1.txt
4
0.000u 0.000s 0:00.00 0.0%	0+0k 0+0io 0pf+0w
UNIX> time ./Graph4 < G2.txt
41
0.000u 0.000s 0:00.00 0.0%	0+0k 0+0io 0pf+0w
UNIX> time ./Graph4 < G3.txt
531372800
0.001u 0.000s 0:00.00 0.0%	0+0k 0+0io 0pf+0w
UNIX>

Grading

This was worth 15 points, and you started with 15 if you had one of the correct working frameworks. After that, you got deductions. For example, if you used the DFS, but didn't memoize, you lost three points.

If you didn't start off with a working framework, then I simply assigned some points for code that looked like it would at least compile, or maybe do something reasonable. Let me give you an example. Here's an answer that is similar to some of yours:

long long Graph::Num_Paths(int from, int to)
{
  int rv;
  int i, j;
  vector <int> P;
 
  for (i = 0; i < Adj.size(); i++) {
    for (j = 0; j < Adj[i].size(); j++) {
      if (Adj[i][j] == to) {
        P.push_back(Adj[i][j]);
      } else {
        Paths[j]++;
      }
    }
  }

  for (i = 0; i < P.size(); i++) {
    rv += Paths[P[i]];
  }
  
  return rv;
}

This answer is worth about three points to me. It should compile, but it doesn't make much sense. There are small problems that I attribute to time pressure and stress. When I'm grading answers like this one, these small problems don't mean much to me, and they don't factor into my assignment of points, although if there are ten of these, then they do factor in. (And I'll say that they do factor into answers that are more correct. For example, if you give one of the good answers above, and you don't initialize your variables, I will take off a point).

rv is never initialized.
path is never initialized.

There are other small mistakes that show a lack of attention to the problem:

rv is an integer rather than a long long.
from is never used.
Incident is never used.

And there are much bigger problems that make this seem as though the student is just putting down code that uses the variables and does something graph-like, but also make it seem like the student doesn't really understand the problem or the solution:

There's no graph traversal here -- just a double-for loop that runs through each element of each adjacency list in order.
The push_back() call is always pushing back Adj[i][j], which is equal to to. That has nothing to do a number of paths.
Why would paths[j] be incremented? j is the variable that is being used to traverse the adjacency list, and it goes from 0 to the size of the list (minus one). This variable has no meaning if considered to be the id of a node, which is how it is being used, by incrementing paths[j].
What does the vector P have to do with anything?

So, I would assign this 3 out of 15, for doing something graph-like, but nothing that seems like the student understands the problem or the proper solution. On your exam, I'll say "Please see the answer." That means that your solution falls into this category.

Question 5

This is very similar to (and much easier than) the PartisanGame topcoder problem that I assigned in lab. That problem had different vectors for Alice and Bob, and the constraints were too big that you could simply use dynamic programming for P. Here, the constraints are much smaller, and you can simply use dynamic programming.

The recursion follows my hints -- try each value of s and recursively call Stones(P-s, S). If that returns that the caller loses, then whoever calls Stones(P, S) will win. If there is no value of s that works, then return that the caller loses.

You have to memoize to make it work fast enough.

Here's my answer, in Stones.cpp. I've added a main() which reads the parameters from standard input, so you can test it.

#include <string>
#include <vector>
#include <iostream>
#include <cstdio>
#include <cstdlib>
using namespace std;

class Game {
  public:
    string Stones(int P, vector <int> &S);
    vector <string> Cache;
};

string Game::Stones(int P, vector <int> &S)
{
  int i;

  /* If the cache is empty, create it. */

  if (Cache.size() == 0) Cache.resize(P+1, "");

  /* Get the return value from the cache if it's there. */

  if (Cache[P] != "") return Cache[P];

  /* Otherwise, use recursion to see if there is any value
     of s that will enable the caller to win. */

  for (i = 0; i < S.size(); i++) {
    if (P-S[i] >= 0 && Stones(P-S[i], S) == "Lose") {
      Cache[P] = "Win";
      return "Win";
    }
  }

  /* If there is no such value, return that you are losing. */

  Cache[P] = "Lose";
  return "Lose";
}

/* Here's a main that lets you test it. */

int main()
{
  int P;
  int s;
  vector <int> S;
  Game G;

  cin >> P;
  while (cin >> s) S.push_back(s);
  cout << G.Stones(P, S) << endl;
}

Here we test a few:

UNIX> g++ -o Stones Stones.cpp
UNIX> echo 5 1 | Stones
Win
UNIX> echo 4 1 | Stones
Lose
UNIX> echo 5 2 | Stones
Lose
UNIX> echo 5 2 3 | Stones
Lose
UNIX> echo 5 2 1 | Stones
Win
UNIX> echo 1000 7 3 11 | Stones
Lose
UNIX> echo 1000 7 3 10 | Stones
Win
UNIX>

Grading

This one is also 15 points, and like the other one, if you have a generally correct framework, you start with 15 and get deductions. If your code isn't close, I gave you 5 points if you had recursion and a cache, and 3 points if you only had recursion.