CS302 2023 Final Exam
December 12, 2023. James Plank. 120 minutes.
The exam was done on Canvas with question banks, so this is an example exam.
Please do all questions. Although it says that there are 11 questions, in my view there are 7:
- Q1 is to enter your username, and Q2 is if you want to make comments to me, so these aren't real questions.
- Q3 through Q8 are each real questions, and when I did them, they all took roughly the same amount of time.
- Q9-Q11 are three parts of the same question -- make sure you read Q10 and Q11 before you start to answer Q9
Budget your time wisely. In particular, you may want to do Questions 3, 5, 6, 7 and 8 before you do Questions 4, 9, 10 and 11. Try not to let time slip away from you in question 4.
Finally -- you can use Question 2 for scratch space. You may find that helpful, for example, in Question 3, part D."
Question 1 - 0 Points
Please enter your UTK username/netid. For example, mine is jplank.
Question 2 - 0 Points
If you feel the need to make comments on your answers, please do so here, rather than in the answer space for the question. You may leave this blank.
Question 3 - 20 Points
Part A
When you implemented merge sort in lab, I recommended the following recursive prototype:
void recursive_sort(vector <double> &v, vector <double> &temp, int start, int size, int print);
|
Suppose I call recursive_sort(v, tmp, 32, 16, 0).
This is going to make two recursive calls. Please tell me start and size
are in these two recursive calls:
Start: _____ Size: _____
Start: _____ Size: _____
Part B
Suppose I call recursive_sort(v, tmp, 4, 4, 0), and v is as follows:
93 49 31 15 71 26 59 10
This is going to make two recursive calls. Right after the second of these returns,
please enter v (enter numbers each separated by a space):
________________________________
Part C
When I call quicksort, here is my input vector:
86 99 86 98 2 47 54 3 36 66 76 14 34
You are using the median-of-three pivot selection algorithm. What is the pivot? _____
Part D
When you implemented quicksort, I recommended the following prototype for the recursive
procedure:
void recursive_sort(vector <double> &v, int start, int size, int print)
|
I call recursive_sort(v, 0, 13, 0), and v is:
74 88 88 80 28 74 15 99 74 74 74 88 28
74 is the pivot. You will make two recursive calls. What is start and size
in each recursive call?
Start: _____ Size: _____
Start: _____ Size: _____
Part E
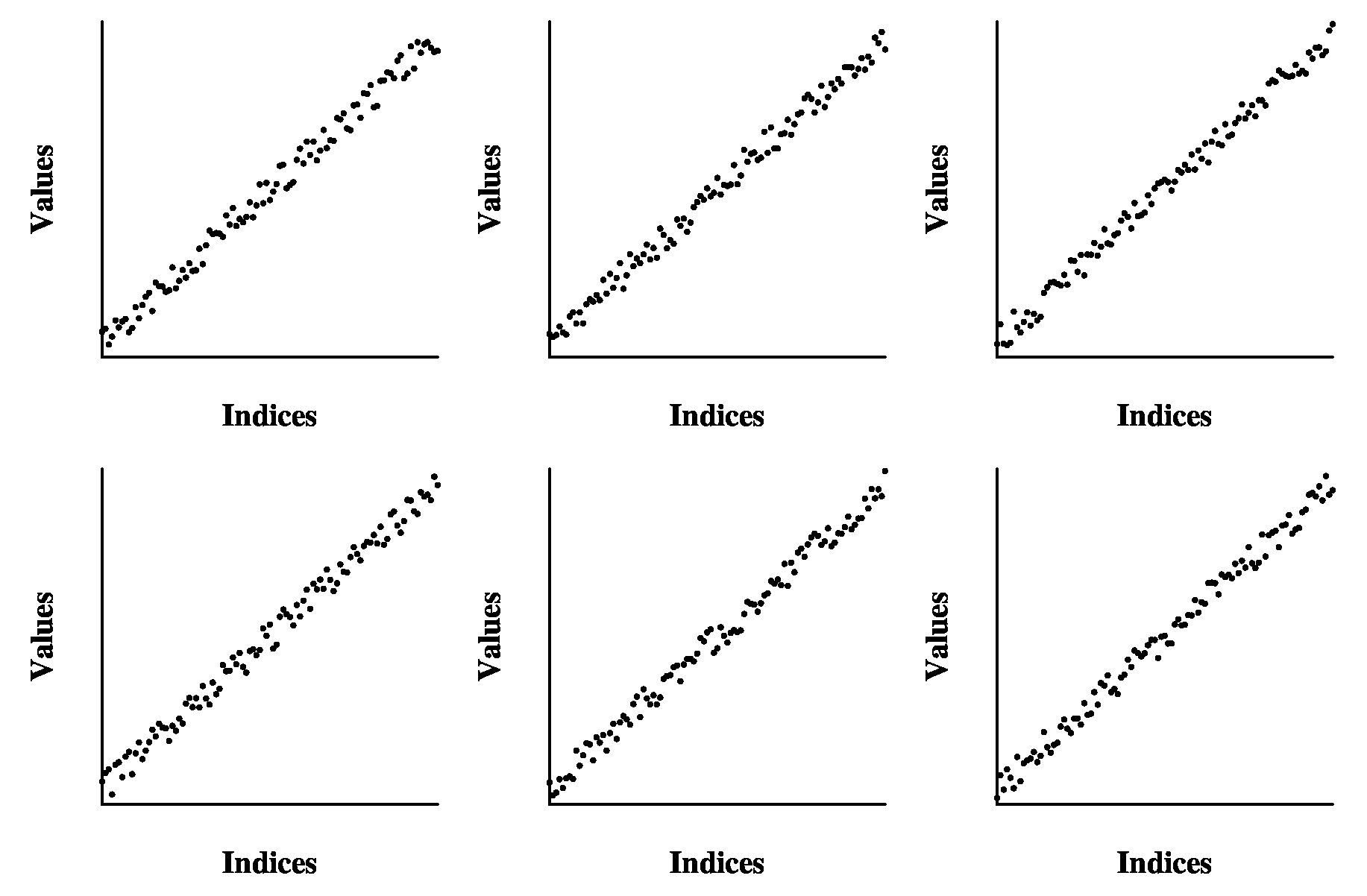
I need to write a sorting procedure, and I am told that my vectors are going to look like
the following graphs:
What sorting algorithm should I use to sort them? __________________
If the vector has n elements, when is the running time of the best algorithm for sorting them? __________________
Question 4 - 20 Points
For each problem below, I want you state the graph algorithm that you
would use to solve the problem, and if you know the running time,
state that. If you don't know the running time (e.g. Network Flow),
then just put an X for the running time. By the way, here are the
graph algorithms that we have studied in this class. You can use the abbreviations
given in your answer:
- DFS: Depth-First Search
- BFS: Breadth-First Search
- DA: Dijkstra's Algorithm
- NF: Network Flow
- MST: Minimum Spanning Tree
- TS: Topological Sort
Hint -- if the algorithm doesn't pop out to you, figure out what in the problem are nodes
and what are edges. Draw yourself an example graph for the
problem, and come up with the answer for that graph. That will help you identify which
algorithm is used to generate the answer.
Part 1:
I am the head of a transportation logistics company. We have two divisions -- air and train. Each of these divisions keeps the following information on cities and the routes between them. Cities are endpoints, where we can store goods. Routes may exist between two cities in either of the divisions. For each route, there is a time to travel the route, and a cost that it takes to travel the route.
Suppose I need to get goods from city A to city B, and I want to do it in cheapest manner, money-wise. Which algorithm should I use? _______________________
Suppose there are C cities and R routes. What is the running time of the algorithm? _______________________
Part 2:
A new management regime takes over from part 1, and dictates that every plane or train trip will cost $1,000. I need to get goods from city A to city B, and I want to do it in cheapest manner. Which algorithm should I use? _______________________
What is the running time? _______________________
Part 3:
A newer management regime takes over, and the costs of the routes return to
what they were in Part 1. Let's suppose that the cost of going from city A to city B is the same as going from city B to city A.
Management has inflicted another cost cutting measure on us -- we need to cancel as many routes as we can, but still make sure that our goods can get from any one city to another. We want to do this, but we want to make sure that the total cost of all routes is as small as possible. What algorithm do we use? _______________________
What is the running time? _______________________
Part 4:
A terrorist group has decided that they want to make it impossible to have goods go from Bangor, Maine to San Diego, CA. The first thing they will do is bomb all of the airports, so no more plane travel. Then, for each train route, they have determined the cost of bombing that route. What algorithm should they use to figure out which train routes to destroy that will achieve their goals in the cheapest manner? _______________________
What is the running time? _______________________
Part 5:
Question 4: The terrorist group has done their bombings. Some of them have been successful, and some of them haven't. You work for the government and know all of the success or failure of each bombing. You are asked if it's possible to get goods from Seattle to Miami. Which algorithm do you use to make this determination? _______________________
What is the running time? _______________________
Question 5 - 8 Points
Please state the halting problem as I stated it in class, and what has been proven about it. Be precise in your writing. Don't give me crap about Turing machines or things that you may have learned about the halting problem in other classes or on Wikipedia. Please state it as I did in class. Also, don't prove anything. I just want the statement of the problem and what has been proven about it.
Question 6 - 12 Points
The following adjacency matrix is for a weighted, directed graph:
A B C D E F G H
--- --- --- --- --- --- --- ---
A | -- 13 -- 57 23 34 -- 85
B | 67 -- -- 40 12 20 12 51
C | 43 86 -- 71 -- 9 42 80
D | -- -- -- -- 21 60 29 90
E | 85 63 -- 30 -- 95 96 7
F | 11 6 -- 79 -- -- 78 41
G | -- 18 -- 71 52 40 -- 22
H | -- 99 79 27 -- 93 -- --
You are running Dijkstra's algorithm from node A. In the table that follows, we keep track
of the distance vector, the backedge vector, and the first key and first val in the multimap.
I have filled out the starting condition. Please fill out what these values are after the first
two iterations of Dijkstra's algorithm:
|
Starting
state |
After first
iteration |
After second
iteration |
| Distance to A |
0 |
|
|
| Distance to B |
- |
|
|
| Distance to C |
- |
|
|
| Distance to D |
- |
|
|
| Distance to E |
- |
|
|
| Distance to F |
- |
|
|
| Distance to G |
- |
|
|
| Distance to H |
- |
|
|
| Back-edge to A |
- |
|
|
| Back-edge to B |
- |
|
|
| Back-edge to C |
- |
|
|
| Back-edge to D |
- |
|
|
| Back-edge to E |
- |
|
|
| Back-edge to F |
- |
|
|
| Back-edge to G |
- |
|
|
| Back-edge to H |
- |
|
|
| 1st key on multimap |
0 |
|
|
| 1st val on multimap |
A |
|
|
Question 7 - 10 Points
In this problem, when you are asked to specify a path, simply specify the nodes in order,
without any spaces. When you are asked to specify a collection of edges, enter pairs of
nodes separated by a space, such as "AB BC CD".
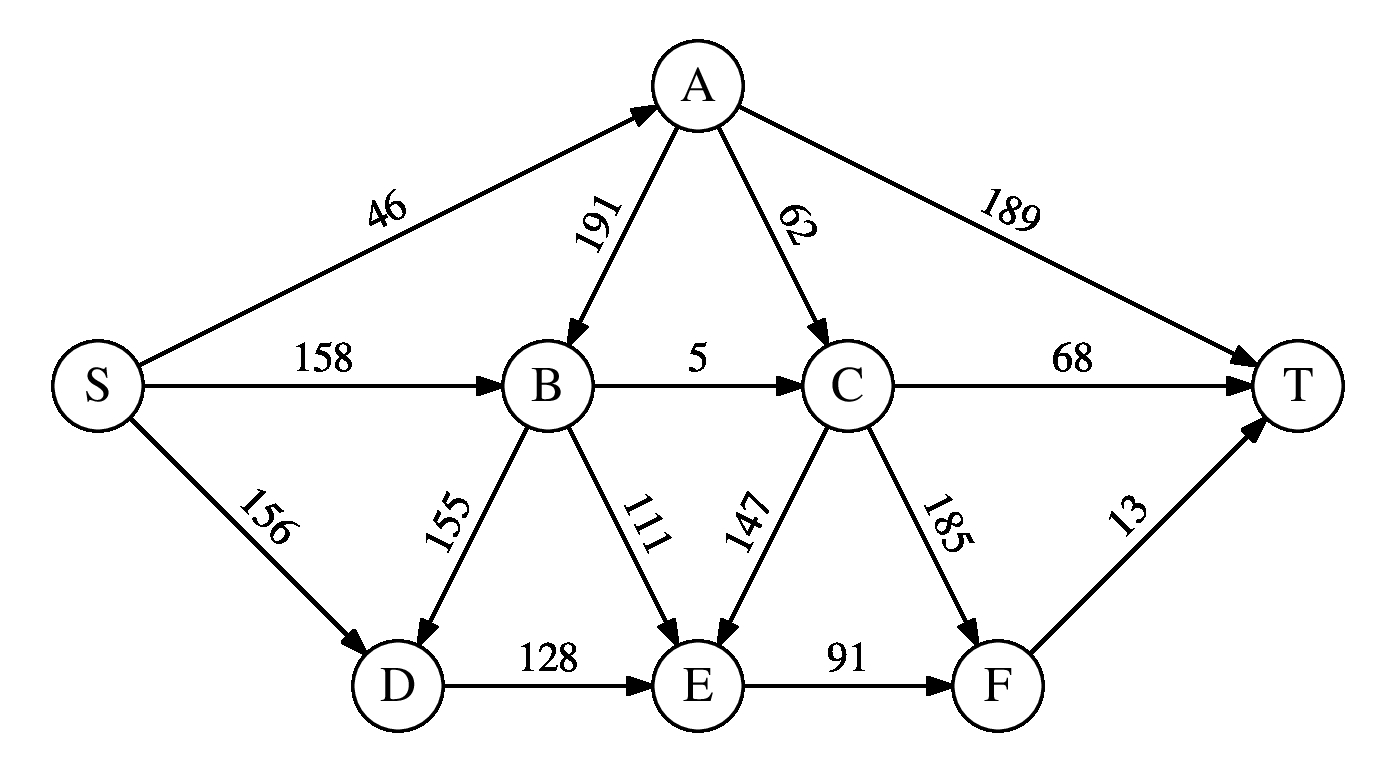
Our application is network flow, and below is a graph whose source is S and whose sink is T:
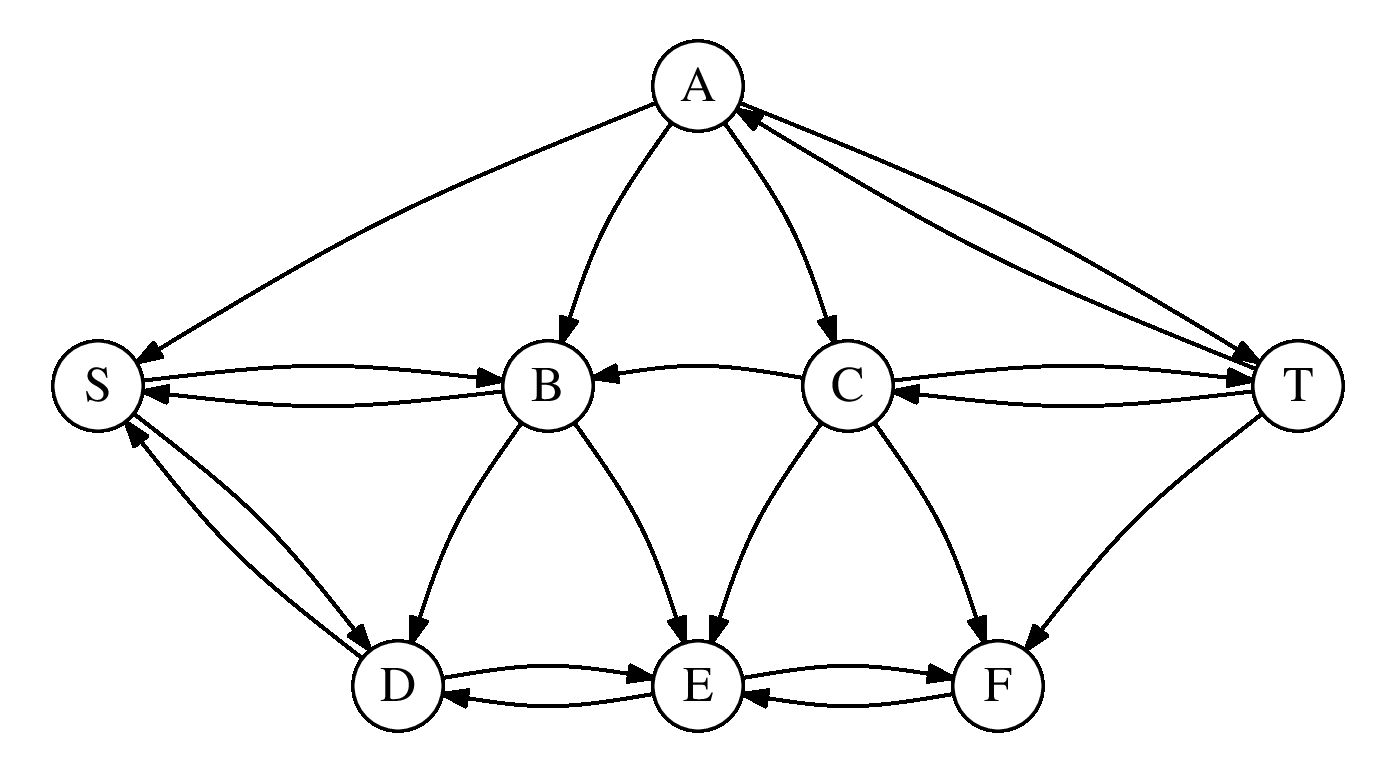
We run the Edmonds-Karp algorithm on this graph, and when we're done, below is the final
residual graph:
Part A
What is the first augmenting path in the algorithm? __________________
Part B
What is the minimum cut of the graph? __________________
Part C
What is the maximum flow of the graph? __________________
Question 8 - 10 Points
In the following code, I enter an unweighted, undirected graph on standard input by simply listing
edges as from, to on standard input. For example, the graph:
is represented on standard input as:
0 1
2 3
or equivalently as:
1 0
2 3
or:
1 0
3 2
In this code, the method Components() returns the number of connected components in
the graph. It uses the vector C to keep track of the components. I've written everything
for you, except that you need to write DFS(). Here's the code:
#include <vector>
#include <iostream>
using namespace std;
class Graph {
public:
Graph();
int Components();
protected:
vector < vector <int> > Adj;
vector <int> C;
void DFS(int node, int component);
};
Graph::Graph()
{
int from, to;
while (cin >> from >> to) {
if (Adj.size() <= from) Adj.resize(from+1);
if (Adj.size() <= to) Adj.resize(to+1);
Adj[from].push_back(to);
Adj[to].push_back(from);
}
}
int Graph::Components()
{
int i, cn;
C.clear();
C.resize(Adj.size(), -1);
cn = 0;
for (i = 0; i < Adj.size(); i++) {
if (C[i] == -1) {
DFS(i, cn);
cn++;
}
}
return cn;
}
int main()
{
Graph g;
cout << g.Components() << endl;
return 0;
}
Here is the code running:
UNIX> echo 0 1 | ./a.out
1
UNIX> echo 0 1 2 3 | ./a.out
2
UNIX> echo 0 1 3 2 | ./a.out
2
UNIX> echo 0 1 3 2 1 2 | ./a.out
1
UNIX>
Please write DFS() below:
Question 9 - 10 Points
Behold the following definition of a function, fA,B(x,y).
- If x = A and y = B,
then fA,B(x,y) = A+B.
- If x < A and y = B,
then fA,B(x,y) = ( x*y + fA,B(x+1,y) ) % 1,000,000,007
- If x = A and y < B,
then fA,B(x,y) = ( x*y + fA,B(x,y+1) ) % 1,000,000,007
- If x < A and y < B,
then fA,B(x,y) = ( x*y + fA,B(x+1,y) + fA,B(x,y+1) ) % 1,000,000,007
And let g(A,B) = fA,B(0,0).
I have written code for calculating g(A,B), and the only thing that it is missing is
the code for DP::f(x,y). Here it is:
#include <vector>
#include <iostream>
using namespace std;
class DP {
public:
int A, B;
long long g(int a, int b);
long long f(int x, int y);
vector < vector <long long> > Cache;
};
long long DP::g(int a, int b)
{
size_t i;
A = a;
B = b;
Cache.clear();
Cache.resize(A+1);
for (i = 0; i < Cache.size(); i++) Cache[i].resize(B+1, -1);
return f(0,0);
}
int main()
{
int a, b;
DP d;
if (cin >> a >> b) {
cout << d.g(a,b) << endl;
}
return 0;
}
|
Below, please implement DP::f(x,y). It should be the "Step 2" implementation of
dynamic programming.
Question 10 - 7 Points
Now, please write the "step 3" implementation of dynamic programming. For this, I have
changed the class definition to the following:
class DP {
public:
long long g(int a, int b);
};
|
Below, please implement DP::g(a,b).
Question 11 - 3 Points
Now, please write the "step 4" implementation of dynamic programming.
For that, you don't need to change the class definition from "step 3".
You may find it helpful to copy-paste your code from "step 3".
Below, please implement DP::g(a,b).