 |
int main()
{
int i, j, *jp;
jp = &j;
j = 15;
i = *jp;
}
|
Let's list everything that we know about these variables:
main:
push #12 / Allocate the three locals
mov #-4 -> %r0 / jp = &j.
add %fp, %r0 -> %r0
st %r0 -> [fp]
mov #15 -> %r0 / j = 15
st %r0 -> [fp-4]
ld [fp] -> %r0 / i = *jp
ld [r0] -> %r0
st %r0 -> [fp-8]
ret
|
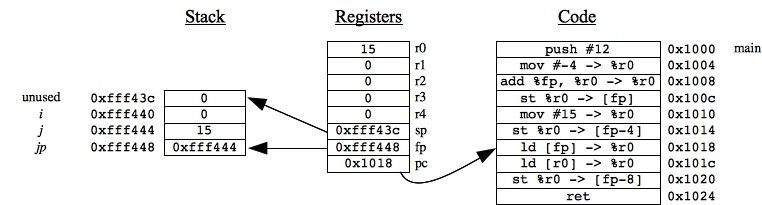
If this is not clear, trace through it in jassem. Here's a reproduction of what I think is the important part of the program -- when you start doing "i = *jp":
 |
We had to manually calculate &j as 0xfff444. You can see that value in jp = [fp]. To calculate *jp, we first load jp into r0:
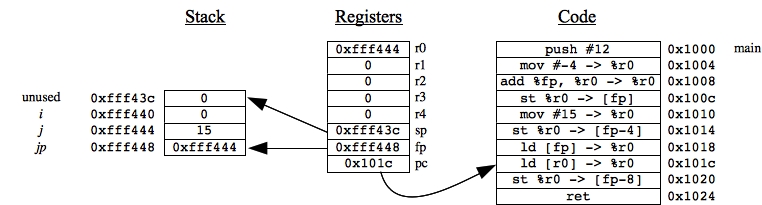 |
And then we load [r0]: that grabs the value in 0xfff444, which is 15 (in jassem, you see it as 0xf, because jassem does everything in hexadecimal):
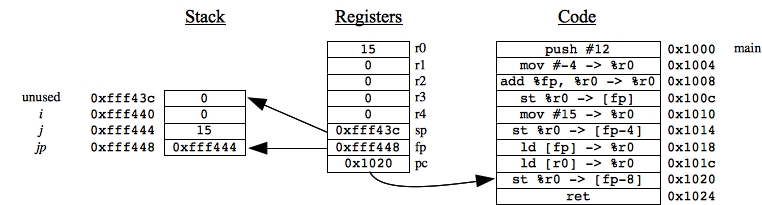 |
Finally, 15 is stored to i (location 0xfff440). I'm not going to draw the picture. Again, you should trace this with jassem.
Let's try a procedure with a pointer. Take a look at pointer2.c:
int a(int *p)
{
return *p;
}
int main()
{
int i, j;
j = 15;
i = a(&j);
}
|
Again, the best thing to do is figure out every variable's address and value:
a:
ld [fp+12] -> %r0 / get p's value
ld [r0] -> %r0 / dereference it
ret
main:
push #8
mov #15 -> %r0 / j = 15
st %r0 -> [fp]
st %fp -> [sp]-- / push &j on the stack
jsr a / and call a()
pop #4
st %r0 -> [fp-4]
ret
|
Once again, you should trace through this in jassem. I'll give you a screen shot this time. One thing that you should do while going through jassem is make sure you can identify every value on the stack. I've done that on the screen shot below, when the code is at the ret statement for a():
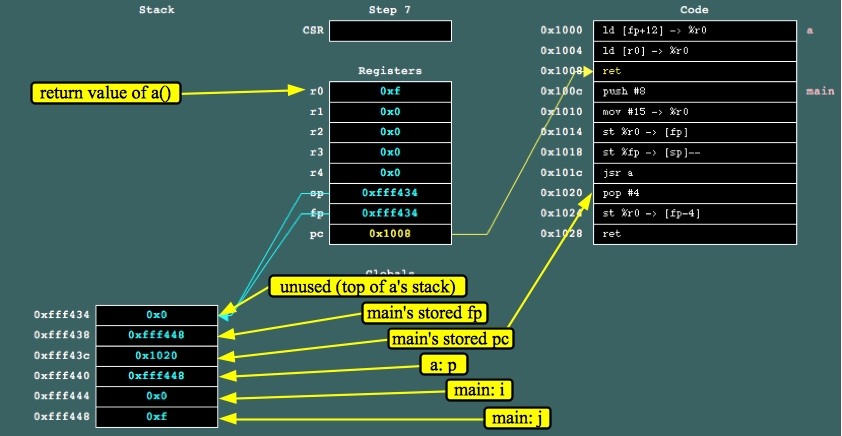 |
void a(int *p)
{
int i;
i = p[0];
i = p[3];
i = p[i];
}
int main()
{
int array[5];
array[0] = 10;
array[1] = 11;
array[2] = 12;
array[3] = 2;
array[4] = 15;
a(array);
}
|
Let's not worry about main() for now. I'm just using the main() to set up memory so that you can trace through a's assembler. Again, let's figure out our variables' addresses and values so that it's easier to come up with the assembler:
And then dereference it. Let's go ahead and put the dereferencing into the equation:
And let's turn that into a tree, just like we did in the last lecture with equations:
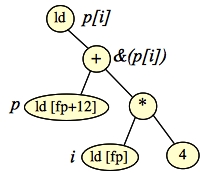 |
I've labeled the nodes so that you can see how we construct &(p[i]) and then we dereference it.
Here's the assembler (in pointer3.jas):
a: push #4 ld [fp+12] -> %r0 / i = p[0] ld [r0] -> %r0 st %r0 -> [fp] ld [fp+12] -> %r0 / i = p[3] mov #12 -> %r1 add %r0, %r1 -> %r0 ld [r0] -> %r0 st %r0 -> [fp] ld [fp] -> %r0 / i = p[i] mov #4 -> %r1 mul %r0, %r1 -> %r0 ld [fp+12] -> %r1 add %r0, %r1 -> %r0 ld [r0] -> %r0 st %r0 -> [fp] ret |
Let's run it in jassem and see what's going on. Again, we're ignoring main() for now. Just step through jassem until you're running a(), just after the "push #4". Again, it's useful to identify everything on the stack:
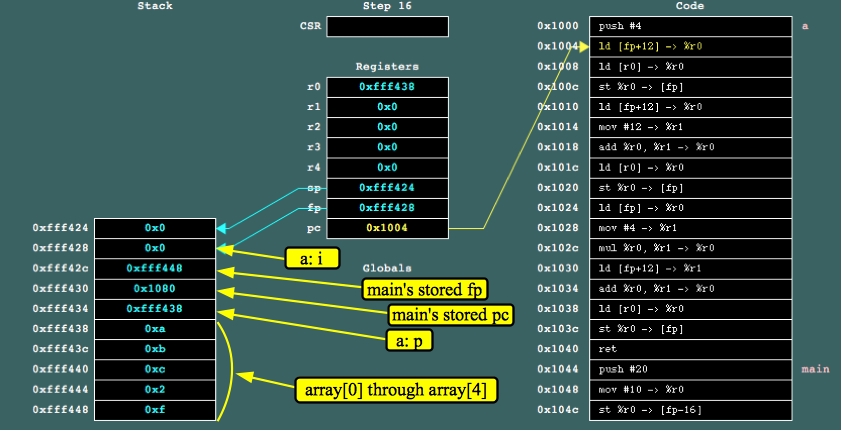 |
Go ahead and trace through that code yourself with jassem. You should see that p[0] is equal to 10 (0xa), p[3] is equal to 2, and because i is set to 2, p[i] is equal to 12 (0xc).
Let's think about main() now. The first thing that it will do is call push #20 to allocate the five integers of array. After that, the compiler knows that:
Armed with this knowledge, setting the elements of array is straightforward. Calling a(array) is a little trickier, but we'll go over it. Here's the rest of pointer3.jas:
main: push #20 mov #10 -> %r0 / Store the values of array st %r0 -> [fp-16] mov #11 -> %r0 st %r0 -> [fp-12] mov #12 -> %r0 st %r0 -> [fp-8] mov #2 -> %r0 st %r0 -> [fp-4] mov #15 -> %r0 st %r0 -> [fp] mov #-16 -> %r0 / Push array onto the stack add %fp, %r0 -> %r0 st %r0 -> [sp]-- jsr a / call a pop #4 ret |
To call a(array), we have to calculate (fp-16) and push that onto the stack. That's done in three lines starting with "mov #-16 -> %r0". The rest is straightforward.
a(int i, int j, int k, int l)
{
int m;
m = i + j + k + l;
}
|
int b(int i)
{
int p[5];
return p[i];
}
|
main()
{
int x;
a(5, 6, 7, 8);
x = b(2);
}
|
Why is it buggy? Because we don't initialize p and we simply return p[i]. The assembler is below (in pointer4.jas):
a: push #4 ld [fp+12] -> %r0 ld [fp+16] -> %r1 add %r0, %r1 -> %r0 ld [fp+20] -> %r1 add %r0, %r1 -> %r0 ld [fp+24] -> %r1 add %r0, %r1 -> %r0 st %r0 -> [fp] ret | b: push #20 ld [fp+12] -> %r0 mov #4 -> %r1 mul %r0, %r1 -> %r0 mov #-16 -> %r1 add %r0, %r1 -> %r0 add %r0, %fp -> %r0 ld [r0] -> %r0 ret | main: push #4 mov #8 -> %r0 st %r0 -> [sp]-- mov #7 -> %r0 st %r0 -> [sp]-- mov #6 -> %r0 st %r0 -> [sp]-- mov #5 -> %r0 st %r0 -> [sp]-- jsr a pop #16 mov #2 -> %r0 st %r0 -> [sp]-- jsr b pop #4 st %r0 -> [fp] ret |
The implementations of a() and main() are straightforward, so I won't bother commenting on them. In b(), we allocate the 20 bytes for p on the stack, and we know that p points to element p[0], which is at address (fp-16). Thus, to access p[i] we need to do:
Let's draw that as a tree:
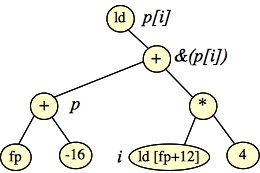 |
Before turning that into code, we can note that addition is associative, so we can reorganize the tree so that it represents the equivalent equation:
| [ fp + (-16 + 4*[fp+12]) ] |
|
That's how we get the assembly code for b() above, which doesn't need to use r2, and therefore doesn't have to do any spilling.
A program like this one is going to run differently from machine to machine, according to how each machine's assembly code is defined and how each compiler maps to that assembly code. On our machine, we can trace through it deterministically. Suppose I asked on an exam, "What is the value of x when main() returns?" You'd have to trace through it to figure it out.
Let's do so with jassem. I'll only give three screen shots. The first is right before a() returns:
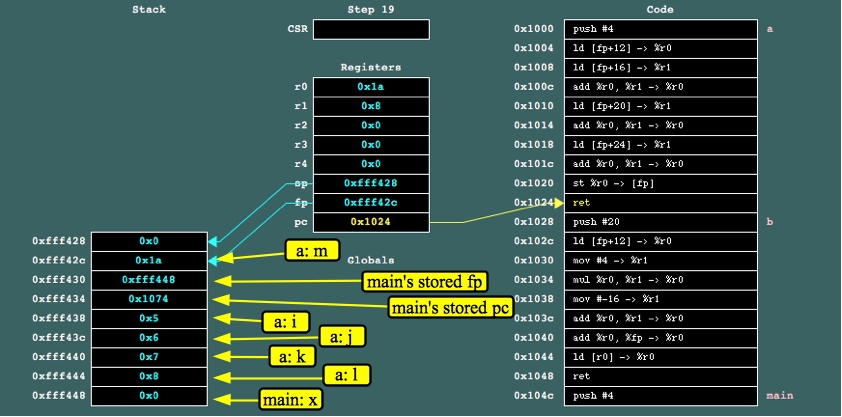 |
You can double check: 5+6+7+8 = 26 = 0x1a.
Now, after the return statement and "pop #16", the state of the system is as pictured:
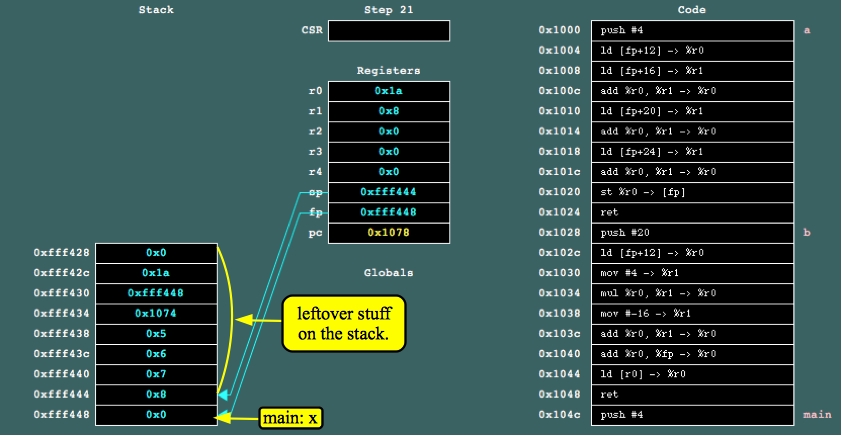 |
We go ahead and push the value 2 onto the stack and call b(). b() calls "push #20" and now the state of the system is as pictured:
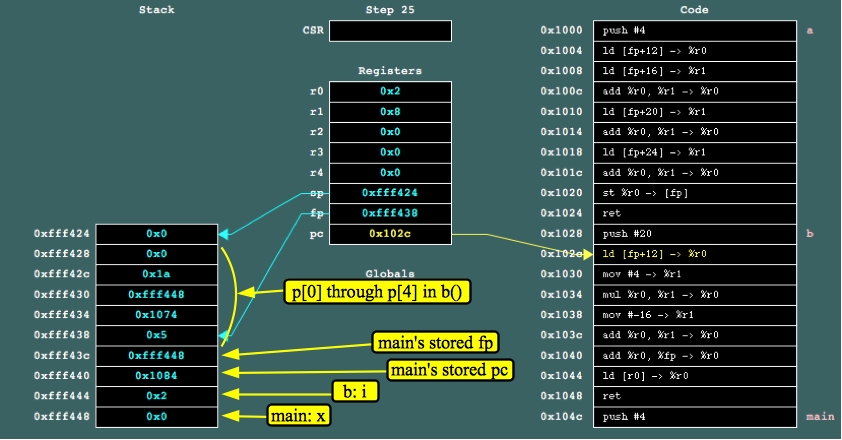 |
Since we didn't initialize the values of p, they are leftover from the previous call to a. Actually, who really knows what p[0] would be, since jassem assumes that memory is all zeros when it starts up.
So b() will return p[2], which is 0xfff448, and the answer to the question is that at the end of main(), x will have the value 0xfff448.
main()
{
int *a, a2[3], i;
i = 6;
a = &i;
a2[1] = i+2;
*a = 2;
*(a2+i) = i+5;
}
|
We'll start with "push 20", and we can locate our variables as follows:
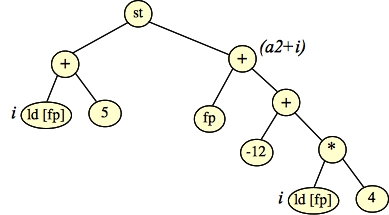 |
We'll have to use three registers to execute that, so we'll have to spill r2 at the beginning. Here's the assembler (pointer5.jas):
main: push #20 / Allocate locals and spill r2 st %r2 -> [sp]-- mov #6 -> %r0 / i = 6 st %r0 -> [fp] st %fp -> [fp-16] / a = &i mov #2 -> %r0 / a2[1] = i+2 ld [fp] -> %r1 add %r0, %r1 -> %r0 st %r0 -> [fp-8] mov #2 -> %r0 / *a = 2 ld [fp-16] -> %r1 st %r0 -> [r1] ld [fp] -> %r0 / *(a+i) = i+5 mov #5 -> %r1 add %r0, %r1 -> %r0 ld [fp] -> %r1 mov #4 -> %r2 mul %r1, %r2 -> %r1 mov #-12 -> %r2 add %r1, %r2 -> %r1 add %fp, %r1 -> %r1 st %r0 -> [r1] ld ++[sp] -> %r2 / Unspill and exit ret |
int x(int **p, int i, int j)
{
return p[i+2][j-2];
}
main()
{
int a[3], b[3], c[3];
int *d[3];
int e;
a[0] = 1; a[1] = 2; a[2] = 3;
b[0] = 4; b[1] = 5; b[2] = 6;
c[0] = 7; c[1] = 8; c[2] = 9;
d[0] = a; d[1] = b; d[2] = c;
e = x(d, 0, 3);
}
|
Let's delay thinking about main() right now. It sets up d so that it is an array of three arrays, each of which has three elements. Moreover, d[i][j] is equal to i*3+j+1. So, when we run this, e will be set to d[2][1] = 8.
In x(), let's go ahead and build up the return value:
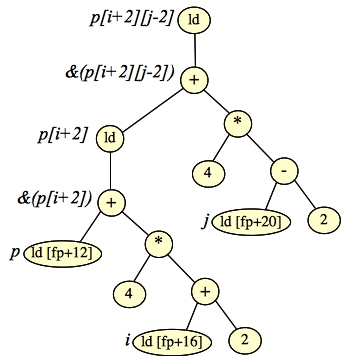 |
Let's implement x() by doing a post-order traversal which is right-to-left rather than left-to-right. We need to use r2. It's in pointer6.jas
x: st %r2 -> [sp]-- / Spill r2 ld [fp+20] -> %r0 / Do the right part of the tree. mov #2 -> %r1 sub %r0, %r1 -> %r0 mov #4 -> %r1 mul %r0, %r1 -> %r0 mov #2 -> %r1 / Do the left part of the tree ld [fp+16] -> %r2 add %r1, %r2 -> %r1 mov #4 -> %r2 mul %r1, %r2 -> %r1 ld [fp+12] -> %r2 add %r1, %r2 -> %r1 ld [r1] -> %r1 add %r0, %r1 -> %r0 / Add them up ld [r0] -> %r0 ld ++[sp] -> %r2 / Unspill r2 ret | main: push #52 st %g1 -> [fp-48] / Do a[0] through c[2]. mov #2 -> %r0 st %r0 -> [fp-44] mov #3 -> %r0 st %r0 -> [fp-40] mov #4 -> %r0 st %r0 -> [fp-36] mov #5 -> %r0 st %r0 -> [fp-32] mov #6 -> %r0 st %r0 -> [fp-28] mov #7 -> %r0 st %r0 -> [fp-24] mov #8 -> %r0 st %r0 -> [fp-20] mov #9 -> %r0 st %r0 -> [fp-16] mov #-48 -> %r0 / d[0] = a add %fp, %r0 -> %r0 st %r0 -> [fp-12] mov #-36 -> %r0 / d[1] = b add %fp, %r0 -> %r0 st %r0 -> [fp-8] mov #-24 -> %r0 / d[2] = c add %fp, %r0 -> %r0 st %r0 -> [fp-4] mov #3 -> %r0 / Push the arguments in reverse order st %r0 -> [sp]-- st %g0 -> [sp]-- mov #-12 -> %r0 add %fp, %r0 -> %r0 st %r0 -> [sp]-- jsr x / call x and set e pop #12 st %r0 -> [fp] ret |
I'm not going to go over main() -- you have the reference material in this lecture to figure it out, and I urge you to do it, especially the setting of d[0] - d[2], and the procedure call.
Go ahead and run jassem on it. Here's the stack just before the call to x(). I've labeled every byte of the stack for you:
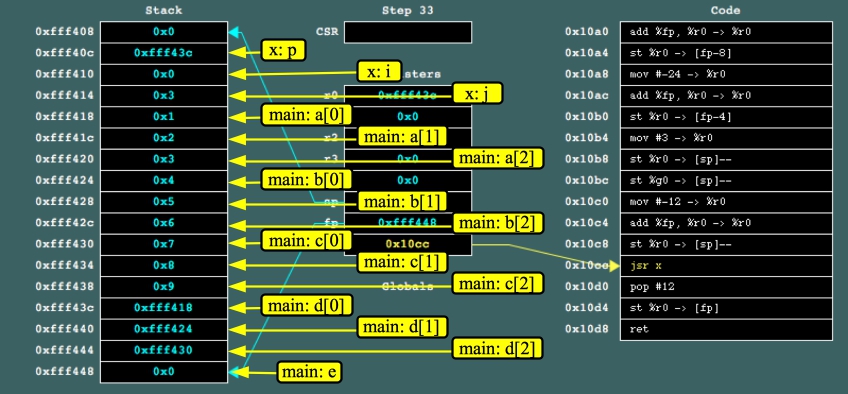 |
I don't think there's much point in putting more screen shots here -- instead, step through the code so that you can see how the element in 0xfff434 (d[2][1]) gets returned.