CS494 Lecture Notes

CS494 Lecture Notes - A-Star

James S. Plank
Directory: /home/plank/cs494/Notes/A-Star
Original notes: February, 2015
Most recent revision: Mon Aug 30 15:33:16 EDT 2021

Introduction and Motivation

A-Star (yes, you can write it A*, but I prefer to write it out. I'm old) is a shortest path algorithm which tweaks Dijkstra's shortest path algorithm to get some drastic performance gains. There are some great resources for A-Star on the web, and I urge you to read one of them (especially the first one).

Amit Patel's series of pages on A-Star are here. They are wonderful.
Mr. Patel has written another set of pages here.
Of course, there's Wikipedia.

The problem is as follows: You want to find the shortest path from node Start to node End in a directed, weighted graph. The idea behind A-Star is simple and elegant, and it is most easily explained with respect to Dijkstra's algorithm. With Dijkstra, you maintain a set of closed nodes: these are the nodes for which you already know the shortest paths from Start. You also maintain a multimap of open nodes ordered by their shortest known distance from Start. At each step, you are assured that the first node in the multimap, let's call it n, is one that you can remove from the open set and add to the closed set. At the same time, you look at each edge from n, and see if you can add or update any nodes in the open set, as a result of taking a path through n to these nodes. You continue in this manner until End is in the closed set. Then you're done.

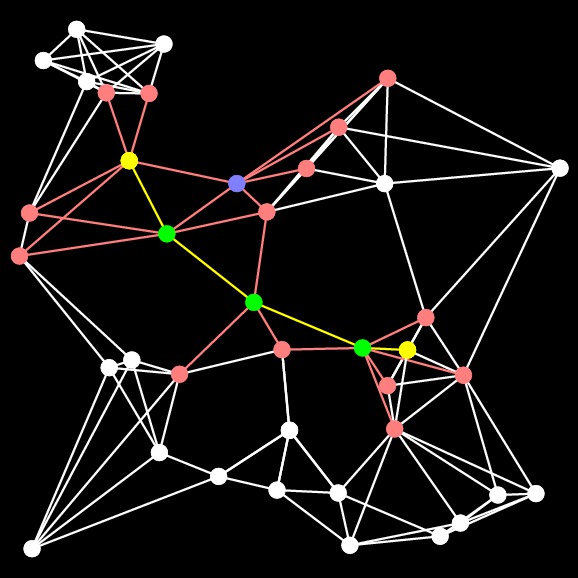
Let's pause here for an example. Let's consider the following graph, where the Start node is the yellow one on the left, and the End node is the one on the right:

On the first step of Dijkstra's algorithm, we add all of the nodes directly connected to Start to the open set. I'll do that by coloring the edges and nodes red:

The nodes in the open set are ordered by their distance to Start. What Dijkstra's algorithm does is select the closest node in the ordered set -- we know that there is no node in the open set that is closer, so we can remove the node from the open set and add it to the closed set. I'll show that by coloring the node blue. We then traverse the node's adjacency list and if it is connected to any nodes that aren't in the open set, then it adds them to the open set. If it is connected to a node that is in the open set, then it considers that currently best known distsnce from Start to that node. If going through the new node makes a shorter path, then the best distance to the node is updated (when we implement this, we use a multimap for the open set, and if we update a distance, we have to remove the node and reinsert it with its new distance). Here's the graph after adding the first node from the open set to the closed set:

We repeat this process until End is put into the closed set. Here's the next step. You'll notice when you eyeball the graph that this is really a poor choice for the next node, because there's no way that this node can be on the shortest path:

This is the fundamental weakness of Dijkstra's algorithm that A-Star attacks. To hammer it home further, here is Dijstra's algorithm after 50 steps:

You'll note that there are three basic routes through the graph, and Dijkstra's algorithm is considering all of them, because it orders nodes by their distance to Start.

Let's look at A-Star after 50 steps:

It has already found the shortest path! And you'll notice that there are several nodes (e.g. the second one chosen by Dijkstra's algorithm) that never made it out of the open set.

Let's see how A-Star works!

The mechanics of A-Star

With A-Star, you assign an extra value to each node. This is the estimated distance from that node to End. We will call it H(n) for each node n. To make the algorithm work, this distance must be less than or equal to the node's actual distance to End. Now, when you add a node to the multimap from Dijkstra's algorithm, instead of adding it based on the distance from Start, you add it based on the distance from Start, plus the estimate of the distance to End.

As of this writing, I have taught this lecture 7 times, and I still find these next paragraphs difficult to teach and understand. But I will try, and I will illustrate with an example.

The algorithm works in a very subtle way. With Dijkstra's algorithm, you know when you add a node to the closed set, you know the shortest path to that node. That is not true with A-Star, and that is a little confusing. In fact, with A-Star, you may need to process nodes more than once, so there actually isn't a true "open set" or "closed set". For the moment, though, let's continue to think that way.

With A-Star, consider the actual shortest path, and consider the first node on that path that is in the open set. When you move that node to the closed set, you know the shortest path to that node (because it comes from Start). Moreover, you are guaranteed to move that node to the closed set before you put End into the closed set. Why? Because the distance from Start plus the estimate to End has to be less than any other path to End.

Continuing by induction, you have to put every node on the shortest path into the closed set before you put End into the closed set. This means that when you actually put End into the closed set, you have found its shortest path.

Why do we have this guarantee? Because our estimates are always correct or low.

I won't explain this any further yet. Instead, let me repeat the specification of A-Star in a slightly different way:

The nodes in the open set are ordered by: (best known distance from Start) + (estimated distance to End)
At each step, you add the best node in the open set to the closed set and process its egdes.
For every node in the closed set that is on the shortest path, you will process that node before you process the End node.
Therefore, When you put End into the closed set, you will know the shortest path to it.

What A-Star does to Dijkstra's algorithm is give preference on the multimap to nodes that are likely to belong on the shortest path from Start to End. The cool thing is that when End is the first node in the multimap, you are assured that you have found the shortest path to it!

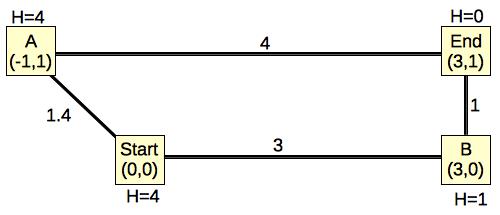
Let's take a really simple example:

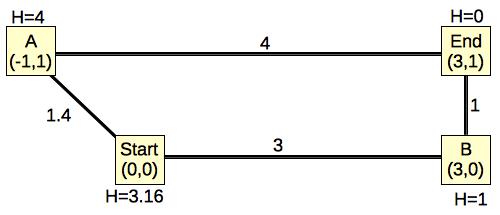The edges are weighted by their Euclidean distances, and I have labeled each node's H value to be its Euclidean distance to End. It should be clear that the actual path length from any node to End will have to be greater than or equal to its H value. In this example, only Start's path length is greater than its H value. The rest are equal.

When you run Dijkstra's algorithm on this graph, you go through the following steps:

Add Start to the closed set. Nodes A and B are added to the multimap, with distances of 1.4 and 3 respectively.
Node A is at the beginning of the multimap, so you remove it and add it to the closed set. You add End to the multimap with a distance of 5.4.
Node B is at the beginning of the multimap, so you remove it and add it to the closed set. The path to End has been improved to 4, so you replace End in the multimap to have a distance of 4.
Finally End is at the beginning of the multimap, so you know its distance is 4. The end.

Now, let's see how A-Star works.

Add Start to the closed set. Nodes A and B are added to the multimap, but instead of using their distances as keys, you use their distances plus H values. Therefore, A has a value of 5.4, and B has a value of 4. You still maintain their actual distances from Start, because you'll need that in subsequent calculations.
Node B is at the beginning of the multimap, so you remove it and add it to the closed set. You add End to the multimap with a distance of 4.
End is now at the beginning of the multimap, so you know its distance is 4. You never had to visit A, because you knew that the path to End through A has to be greater than or equal to 5.4.

The two drawings below illustrate the ending state of the two algorithms:

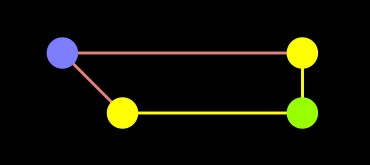Dijkstra
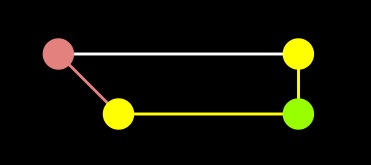A-Star

As you can see, the difference is the fact that the A node is in the closed set with Dijkstra, but in the open set with A-star. As a result, the edge from A to end was not processed in A-star.

A second example

Let's do a second example, which is in Harder-Example.odp. (Note to myself: Make printouts of this so that the students can do it themselves with you. Copy this to another file and then go through it interactively. When you make a change, verify with the next screen of the presentation, like you do with B-Tree).

Why the low estimates make it work

Ok -- let's revisit why this works, using the previous example. First, let's look at the graph:

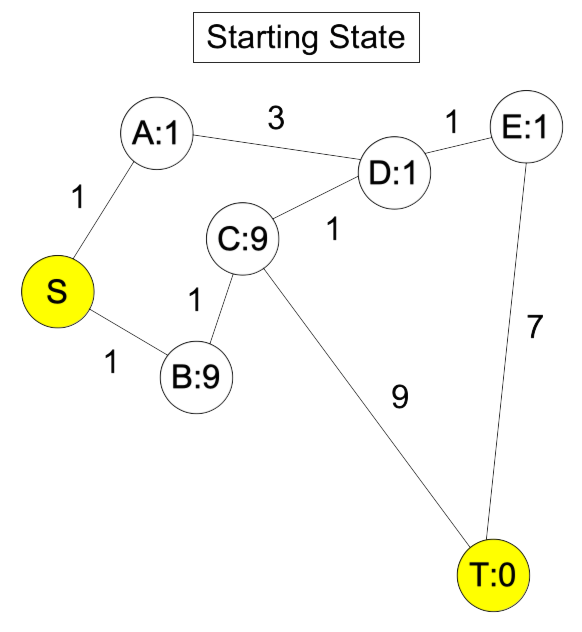The shortest path is S-B-C-T, but because the estimates for A, D and E are so low, the algorithm guides us to S-A-D-E-T. Here's the graph after we put E into the closed set:

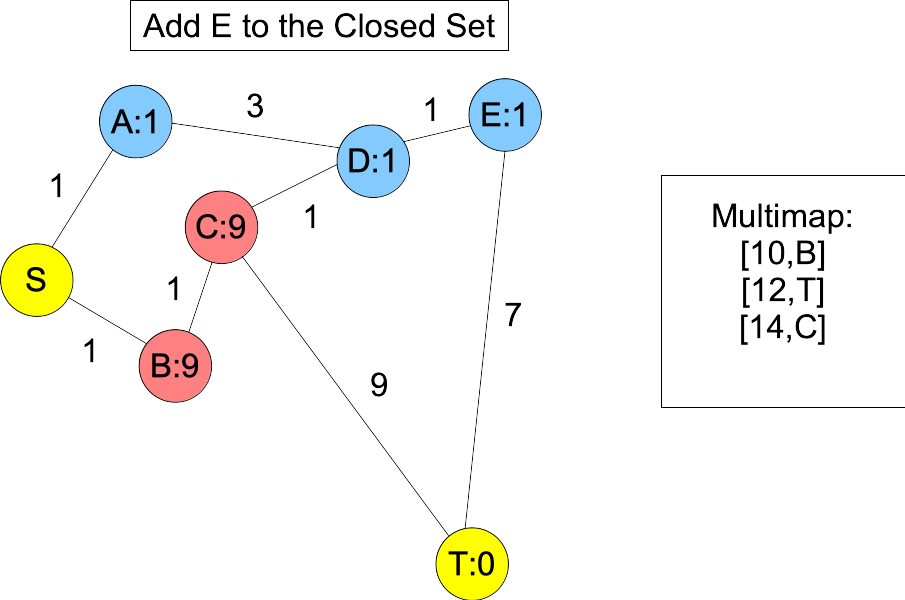You'll note, when we put D and E into the closed set, we don't know the shortest paths to them -- you can get to D with a shorter path: S,B,C,D. However, the next node on the actual shortest path, B, is in the open set and we happen to know its shortest path. Moreover, its distance plus estimate must be less than or equal to the actual shortest path length. Therefore, it will always be in the multimap with a lower value than T. When we add it to the closed set, C becomes the next node on the shortest path in the open set, and you'll note that is is also before T, because its value in the multimap is equal to the actual shortest path length:

Processing Nodes More Than Once?

If you look at the graph above, you'll see that there are two paths of length 11: SBCT and SBCDET. If you delete the edge from C to T, you'll go through the same steps of A-Star, but now you'll have to process D and E a second time. That's a drag, but you should be aware of it.

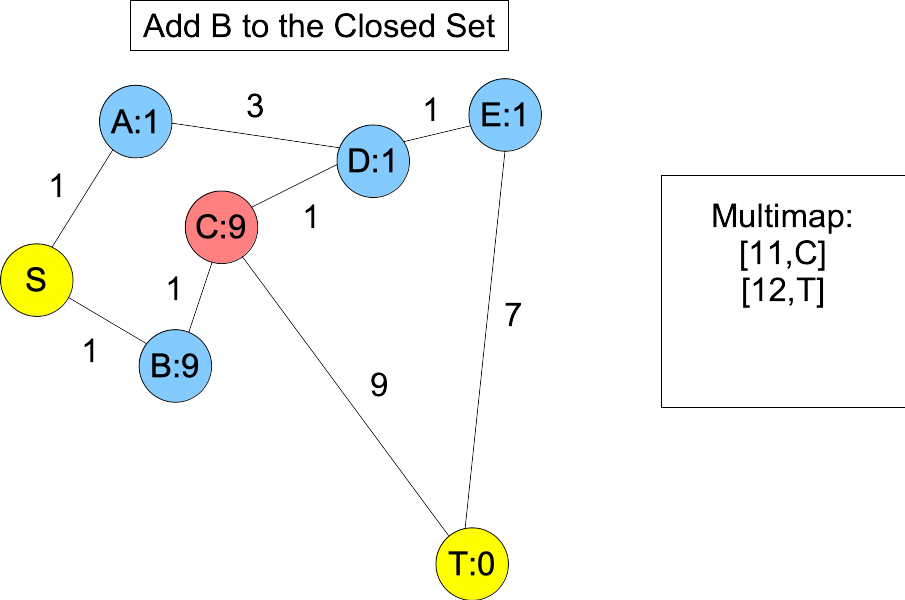You can avoid this by having a consistent heuristic. To be consistent, h() must be such that for every adjacent node X and Y,

h(x) ≤ W(x,y) + h(y)

In other words, a node's estimate can't be greater than (the distance to any neighbor) + (the neighbor's estimate). This is violated all over the place in the graph above, but the most egregious place is with C and D. C's estimate is 9, which is much bigger than 1+1, which is the distance to D and D's estimate.

Fortunately, in the programs below, I'm using a consistent heuristic, so I can keep the "open set"/"closed set" heuristic.

How good do those estimates need to be?

I'm not going to write much here, because the Patel pages above do a fantastic job with it. However, I'll go over a few key points:

If you always set H to zero, you have just turned A-Star into Dijkstra.
So long as each node's H value is less than or equal to its actual distance to End, A-Star will always find the shortest path.
The number of nodes in the closed set will be reduced by having higher, but still legal, H values.
If each node has its actual distance as its H value, and there is only one shortest path, then A-Star will find it without adding any additional nodes to the closed set.

However, if there are multiple shortest paths, your closed set can get pretty big. Here's an example graph using ASCII art:

O -> O -> O -> O -> O -> O -> O -> O
|    |    |    |    |    |    |    |
v    v    v    v    v    v    v    v
O -> O -> O -> O -> O -> O -> O -> O
|    |    |    |    |    |    |    |
v    v    v    v    v    v    v    v
O -> O -> O -> O -> O -> O -> O -> O
|    |    |    |    |    |    |    |
v    v    v    v    v    v    v    v
O -> O -> O -> O -> O -> O -> O -> O
|    |    |    |    |    |    |    |
v    v    v    v    v    v    v    v
O -> O -> O -> O -> O -> O -> O -> O
|    |    |    |    |    |    |    |
v    v    v    v    v    v    v    v
O -> O -> O -> O -> O -> O -> O -> O
|    |    |    |    |    |    |    |
v    v    v    v    v    v    v    v
O -> O -> O -> O -> O -> O -> O -> O

The reason is that for all nodes on the shortest path, the sum of shortest path from Start and the estimate is equal to the path length from Start to End. So this sum is the same for all nodes that are on any shortest path.

To make A-star effective here, you need to tweak either the algorithm or your estimates here -- the Patel page goes into great length on this, and it's fascinating.

If your H values are too big, then you may not find the actual shortest path, but instead one that is hopefully close to the shortest path. That may be good enough for your purposes, and your closed set will be smaller than if you had used better estimates.

Some programs to explore A-Star

I've written a few programs to explore A-Star. Let's start with src/a-star-tester-0.cpp. You call it as follows:

bin/a-star-tester-0 seed xmin ymin xmax ymax nn connections-per-node Dijkstra|A-Star|Nothing print(Y|N|G)

It will create a random graph on the XY coordinate plane bounded by (xmin,ymin) and (xmax,ymax). The graph will have nn nodes and it will be fully connected. Each node will have roughly connections-per-node edges to nearby nodes. The Start node will be on the left side somewhere, and the End node will be on the right side. When the graph is created, you can then run Dijkstra, A-Star, or nothing on it. At the end, if you specify Y, it will print out the graph using the colors above, using jgraph. If you specify G, it simply prints out a text file representation of the graph before runnning the algorithm. If you specify N, it only prints timing information, and the sizes of the open and closed sets. Finally, if you specify 0 as connections-per-node, it doesn't create the graph, but instead reads its text representation from standard input.

Let's try a simple example:

UNIX> bin/a-star-tester-0 106 -10 -10 10 10 40 5 Nothing G > txt/G-40-5-106.txt
UNIX> bin/a-star-tester-0 106 -10 -10 10 10 40 0 Dijkstra N < txt/G-40-5-106.txt
(* Time:          0.000028 *)
(* Path Length:     12.875 *)
(* Closed Set Size:     25 *)
(* Open   Set Size:     10 *)
(* Unvisited Nodes:      5 *)
UNIX> bin/a-star-tester-0 106 -10 -10 10 10 40 0 A-Star N < txt/G-40-5-106.txt
(* Time:          0.000011 *)
(* Path Length:     12.875 *)
(* Closed Set Size:      7 *)
(* Open   Set Size:     14 *)
(* Unvisited Nodes:     19 *)
UNIX>

If you use the jgraph option (and do a little tweaking, as I am wont to do), you get the following pictures of the above calls:

Dijkstra
A-Star

The pictures and the output of the programs convey the same thing -- they have both found the same shortest path from Start to the End. However, Dijkstra's algorithm visits more nodes and edges, and has many more nodes in its closed set. A-Star, on the other hand, is much smarter about its closed set, which only has two nodes that aren't on the shortest path.

(Graph Generation)

This isn't about A-Star, but it is interesting, because generating good relevant graphs was a bit of a challenge.

I'd be remiss if I didn't talk a little about how the program generates its graphs. My intent was to have each node have connections-per-node edges to its closest neighbors. There are some issues with this, of course. First, there is an issue of reflexiveness. Take a look at the rightmost node in the graphs directly above, and suppose that connections-per-node were one instead of five, and suppose that we call the node A, and the one closest to it B. It's pretty clear that A is not the closest node to B, or even one of the four closest nodes to B.

So, what I settled on was the following. I considered the nodes in random order (the order in which they were created). When I considered a node, it may already have had edges on its adjacency list. So, I needed to generate z = (connections-per-node - adjacency.size()) new edges. To do that, I maintained a map of closest nodes, ordered by their distance to the node. It starts empty, and I never let it get bigger than z elements (if it does, I delete the biggest elements on it).

Now, I consider four nodes as candidates for the map:

The node whose x value is largest value smaller than the node's. Let's call this node x_low.
The node whose x value is smallest value greater than the node's.
The node whose y value is largest value smaller than the node's.
The node whose y value is smallest value greater than the node's.

If these nodes aren't already on the adjacency list, and if I haven't visited them before, I insert them into the map. After considering the four nodes, I look at the next node along the given axis. For example, I set x_low to be the node whose x value is largest value smaller than x_low's.

I can stop when the distance along the given axis is big enough. For example, I can stop considering x_low nodes when the distance between x_low and the node along the x axis is bigger than the largest node in the map.

It's hard to do a formal analysis of this, but it should do a decent job of considering a fairly small subset of the nodes, especially when the number of nodes is large and connections-per-node is small. I would probably do better to break up the grid into squares whose sides are sqrt(|V|) or something like that, and then only look for edges within certain squares. I don't have the time to play with it.

When I'm done with this process, I add the nodes in the map to the node's adjacency list (and add the reverse edges, because these graphs are undirected).

At that point, the graph may be disconnected. To connect it, during the graph generation process, I maintain disjoint sets of connected components. Then, after generated the edges above, I connect the graph by going through the following process -- I choose a random node, and find the closest node to it that is not in the same set. Then, I find the closest node to that one that is not in the same set. The logic there is that the first node that I have chosen may be in the "middle" of its disjoint set. However, the node closest to it will be on the "edge" of its disjoint set. So that's a good node to connect with another disjoint set. That part of the algorithm is O(|V|) for each disjoint set.

I'm left with a fully connected graph, and its running time shouldn't be O(|V|²), which is what I was trying to avoid.

Trying to make it faster and better

I have a few modifications to the program. The first is src/a-star-tester-1.cpp, which stores the H value of each node when it is first calculated. The previous program simply calculated it every time it was needed. I don't explore this in these lecture notes, but if you're interested, you should. It's a memory vs. instruction tradeoff, and those are often more subtle than you think.

The second program is in src/a-star-tester-2.cpp, which tries to make H better. What it does is the following: When it needs to calculate a node's H value, it doesn't use Euclidean distance. Instead, it considers every node to which it is incident that is not already in the closed set. It calculates the distance to that node, plus that node's Euclidean distance to End, and sets its H value to the minimum of these values. You should see how that gives you H values that are higher than the Euclidean distance, but still less than or equal to the actual shortest path lengh.

If a node is in the open set, and all of its edges are to nodes in the closed set, then there is no way that the node can be on a shortest path. When we discover such a node, we set its H value to ∞.

Look at a simple example, which is the first graph I showed you:

Using our new calculation, the Start node's H value is 4, rather than 3.16. That is because Start chose its H value to be the minimum distance-plus-H value to A and B, rather than its Euclidean distance. You should see how that results in a higher, but still legal H value.

Obviously, the tradeoff in this program is going to be smaller closed-set size, versus more expensive calculation of H. When I first implemented it, here's the picture I got with the above example:

That doesn't look right, does it? The closed set side is bigger than the previous example. The reason is that I used the algorithm to set End's H value, rather than just setting it to zero. That's a bug, and I discovered it by looking at the pictures. I show this just to highlight how important it is to test your programs as you write them!!!. That program is in src/a-star-tester-2.cpp.

The bug is fixed in src/a-star-tester-3.cpp. Here's the output -- you can see that there is one fewer node in the closed set than in the previous A-Star example:

UNIX> bin/a-star-tester-3 106 -10 -10 10 10 40 5 A-Star N < txt/G-40-5-106.txt
(* Time:          0.000008 *)
(* Path Length:     12.875 *)
(* Closed Set Size:      6 *)
(* Open   Set Size:     14 *)
(* Unvisited Nodes:     20 *)
UNIX>

Using H values that are too high

My final program is src/a-star-tester-4.cpp. In this program, rather than specify "Dijkstra|A-Star|Nothing," you specify a factor. The H value is set to the Euclidean distance multiplied by the factor. This means that factors less than or equal to one will find the shortest paths, but smaller factors will yield bigger closed set sizes. Factors greater than one will have smaller closed set sizes, but they are not guaranteed to find the shortest paths. For example:

UNIX> bin/a-star-tester-4 106 -10 -10 10 10 40 5 1.1 N < txt/G-40-5-106.txt
(* Time:          0.000011 *)
(* Path Length:     12.875 *)
(* Closed Set Size:      7 *)
(* Open   Set Size:     14 *)
(* Unvisited Nodes:     19 *)
UNIX> bin/a-star-tester-4 106 -10 -10 10 10 40 5 2 N < txt/G-40-5-106.txt
(* Time:          0.000015 *)
(* Path Length:     14.672 *)
(* Closed Set Size:      6 *)
(* Open   Set Size:     15 *)
(* Unvisited Nodes:     19 *)
UNIX>

As you can see, that last call didn't find the shortest path. This is the one that it found. When the factors get really high, the program becomes a greedy DFS using only the Euclidean distances as heuristics, and ignoring the effect of the paths to the nodes.

Pretty Pictures of Large Graphs

In this example, I create a 10,000 node graph:

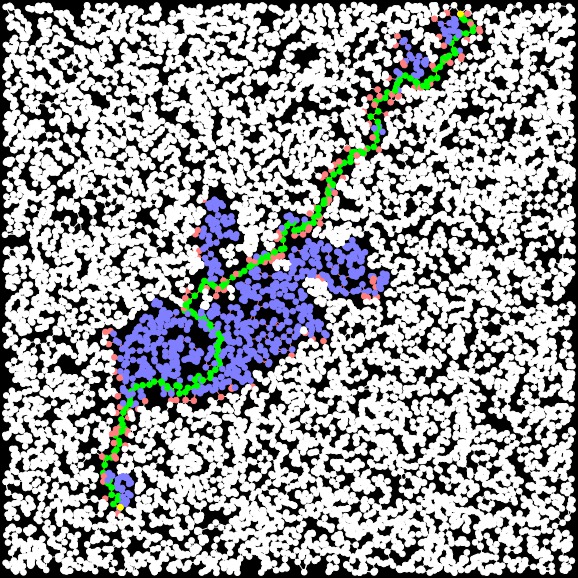
UNIX> bin/a-star-tester-0 1 -10 -10 10 10 10000 3 Nothing G > G-10000-3-1.txt

Below, I show the various programs finding the shortest paths (sometimes):

The graph
Finding the yellow nodes is like finding Waldo...
Dijkstra
Path Length = 30.706.
Time: 0.004342 seconds
Closed Set Size: 9729
A-Star
Path Length: 30.706
Time: 0.002506 seconds
Closed Set Size: 4893

A-Star-3 (improved H)
Path Length: 30.706
Time: 0.002754 seconds
Closed Set Size: 4816
A-Star, Factor = 1.1
Path Length: 30.721
Time: 0.002091 seconds
Closed Set Size: 3971
A-Star, Factor = 2
Path Length: 32.212
Time: 0.000481 seconds
Closed Set Size: 891

A few items of note:

The improvement from Dijkstra to A-Star is impressive!
Although A-Star-3 did improve the size of the closed set, the improvement wasn't enough to offset the complexity of calculating H.
Using a factor of 1.1 reduced the size of the closed set by 19 percent, while it also resulted in a path that was 0.05 percent longer than the optimal one. Its running time was 17 percent faster than our original A-Star.
Using a factor of 2.0 reduced the size of the closed set by a whopping 82 percent, and improved the running time by 81 percent. However, the path it found was 5 percent longer than the optimal one. You can see that the "obstacle" in the graph caused this one the biggest problem. I find this stuff fascinating....

Below, I graph the algorithms on the 100,000 node graph in G100K.txt. The leftmost Y axes are log scale, and you can see the various tradeoffs very clearly:

An A-Star Example -- The "Freeway" Application

The "Arcade Learning Environment" (https://github.com/mgbellemare/Arcade-Learning-Environment) and "OpenAI Gym" (https://gym.openai.com/) implement video games for research on Artificial Intelligents. They present an instance of playing the game as a sequence of observations, and each time an AI Agent is presented with an observation, it must return an action. The Freeway application is an old Atari game where a chicken has to cross a road which has ten lanes of traffic traveling in various directions and various speeds. Here's a screenshot:

In our research, we train spiking neural networks to direct control applications such as video games. In 2020, I needed to learn Python, so I focused on training neural networks for the Freeway application. BTW, if you want to learn about spiking neural networks, please see our group's web site at http://neuromorphic.eecs.utk.edu/. The introductory video -- https://youtu.be/_Ac_PHJyE2Y is four minutes long and does a really nice job of introducing you to spiking neural networks and control applications.

The observations of the Freeway application are brutal -- the old Atari game had 128 bytes of RAM, and that's what you are given. Some research projects use that, and some use the pixel rendering of the game begin played. In our research, we analyzed the RAM to figure out which bytes represented the cars, and which byte represented the Y value of the chicken. We then used these as inputs to training networks.

While working on this, I wanted to know what the "best" performance could be, so I wrote an oracle. The way the oracle works is that it plays the game many times, and each time it plays the came it builds a graph. The nodes of the graph are a combination of the chicken's Y value and the timestep. At each node, you have three choices: up, down and stay. So each node has three edges. The shortest path from (y=0,t=0) to (y=top,t=anything) is the optimal way to play the game with that seed.

There were challenges with this approach. To evaluate each move, I needed to play the game three times. Worse yet, if you arrive at a node in different ways, there's a chance that the same move takes you to a different node. I have an example pictured below:

In this example, "1" means up, "0" means stay, and "2" means down. As you can see, the action out of node (8,14) results in a different edge, depending on how you got to the node. So in my search, I made sure that the same path was always used to get to a node. (You may correctly comment that this means my oracle is not really an oracle. There are only so many hours in the day).

I use A-Star to do the search, and build the graph on the fly. Otherwise, the graph will blow up (it is infinite in size). I didn't try Dijsktra's algorithm, because it would have been too slow, so A-Star was essential. For h(), I simply used the top y value minus the chicken's current y value, divided by the maximum y values that can change on an "up" action. To be honest with you, I'm not sure if that is consistent or not, but it does satisfy the constraint that h() is less than the actual shortest path.

Here's a nice graph from one of the runs:

You can really see the effectiveness of A-Star here -- imagine how many nodes Dijkstra's algorithm would have!

You can see the results of this activity at https://www.youtube.com/watch?v=FKYXuzNVZKg, where I show 25 perfect runs.

As an aside, in https://www.youtube.com/watch?v=B_nQtRMYVIc, I have a video of one of the spiking neural networks. I call this "the scared chicken", because it is super-cautious. It doesn't score well, but it also avoids collisions very actively. If you care it is a spiking neural network with just two input neurons, three output neurons and two synapses.

Another Application of A-Star

This one comes from https://www.gatevidyalay.com/tag/a-algorithm-applications/. You are given one of those puzzles where you have a grid of tiles with one tile missing. The tiles have numbers or represent pictures (I remember vividly having one with a Philadelphia Phillies logo on it that my parents bought me at a Phillies game). You can move any adjacent tile to the empty space, and your goal is to unshuffle the tiles.

The shortest path is the minimum number of moves to get from the current state to the unshuffled state. Like the problem above, you do best to generate the graph on the fly, because it can be huge. The A-Star heuristic of a node is the number of nodes that are in the wrong position.

BTW, a good class presentation would be on problems like this (or from that web site), where you test multiple heuristics for A-Star.

The graph Finding the yellow nodes is like finding Waldo...	Dijkstra Path Length = 30.706. Time: 0.004342 seconds Closed Set Size: 9729	A-Star Path Length: 30.706 Time: 0.002506 seconds Closed Set Size: 4893
A-Star-3 (improved H) Path Length: 30.706 Time: 0.002754 seconds Closed Set Size: 4816	A-Star, Factor = 1.1 Path Length: 30.721 Time: 0.002091 seconds Closed Set Size: 3971	A-Star, Factor = 2 Path Length: 32.212 Time: 0.000481 seconds Closed Set Size: 891