CS494 Lecture Notes - Problem Solving with Network Flow

This lecture highlights four problems from Topcoder that have network flow solutions. All of them rely on minimum cuts in some way for their solutions. In my opinion they are pretty subtle and fascinating.

In Case You Need To Bone Up On Network Flow

Please read the first set of lecture notes on network flow from CS302. In these notes we: To understand this lecture, you'll need to understand the material from the CS302 lecture, so please give it a thorough read before tackling these lecture notes.

#1: Dealing with Huge Edge Capacities: SRM 632, D1, 500-pointer - CandyCupRunningCompetition

First, let me give the pithier explanation of this problem: As with all of these problems, there is a general principle at work. In this problem, the general principle is the following:

If the relative ordering of edge weights will never change, then you don't need to add flow or reverse flow when processing the residual graph. You simply delete the edge that defines the flow for the path. The structure of your simplified residual graph will match the structure of the unsimplified residual graph, and you can use the minimum cut to determine the maximum flow.

Although the writeup of this Topcoder question is cute, it is a network flow problem, plain and simple. You are given a graph with N nodes ane M edges. The edges are numbered 0 through (M-1), and the capacity of edge i is 3i. Your goal is to find the maximum flow from node 0 to node N-1. There's a little subtlety that the edges are bidirectional, which means that you really have two edges between any pair of nodes. The edges share their "candy," though, so again, it's a standard network flow problem that you are solving.

The problem is difficult, because the constraints have M being as big as 2000, and 31999 is not going to fit into a long long.

What I do in these situations is work through some examples to get some inspiration. Let's use the following example graph:

It should be pretty clear that the total flow through this graph is 1+9+81 = 91. Let's process paths through this graph. Start with 0-1-2-3-4, with a flow of one. Here's the residual (I'm showing the forward-edge-weight/backward-edge-weight):

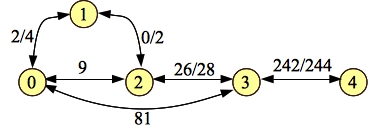Now, let's process 0-2-3-4 with a flow of nine:

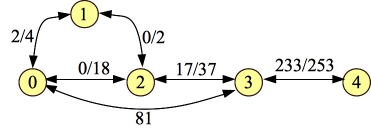And finally 0-3-4 with a flow of 81:

The minimum cut here is equal to the flow -- edges (1-2), (0-2) and (0-3), whose weights sum to 91.

Suppose you have an edge with a value of 3i, for example, 27. How much flow can go through that edge? Well, obviously, 0 and 27. What about smaller values? Those would be 9, 3, 1 and their combinations. That's a max of 13. You'll note that 13 is less than 27/2. This turns out to be true in all cases -- the amount of flow that can go through an edge whose value started at 3i is either exactly 3i, or it is less than 3i/2.

Does that help us? A little. Consider an augmenting path through the residual graph. I will propose that the flow through this path is going to be equal to the edge whose initial weight was the smallest of all the edges on the path. This is regardless of what has happened previously to that edge.

Think about it -- suppose you have an augmenting path that includes the edge whose weight started at 27, and that is the smallest value of initial weight for all edges on the path. Then, the flow through the path will be equal to the flow through that edge.

Let's elaborate more. Supoose that edge has been part of other augmenting paths, and it has had 9, 3 and 1 added to it. Its weight is now 40. The smallest edge whose weight was bigger than 27 is 81, and the only edges that could have been subtracted from it are 27, 9, 3, and 1, which would give it a weight of 41. This means that the edge whose weight started at 81 will always be bigger than the edge whose weight started at 27, regardless of the flows that have been added to them or subtracted from them. You can generalize this, but I won't.

What's the upshot of this? That you only need to keep track of the initial values of the edges, and when you would normally subtract a smaller edge from a larger one, or add a smaller edge to a larger one, you don't have to do the addition or subtraction. The only thing you do when you process a path is delete the edge whose initial weight was the minimum. You will end up with the same residual graph as you would if you were actually doing the addition and subtraction.

Let's work through the example above. We first process the path 0-1-2-3-4, and just delete the minimum edge on each path:

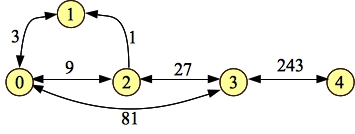Compare this graph to the first residual in the example above, and see how it matches. In particular, if you ignore their weights, then the two graphs are the same. In other words, this graph has the same structure as the original residual graph. That is going to be true for each time we process a path. Here's 0-2-3-4:

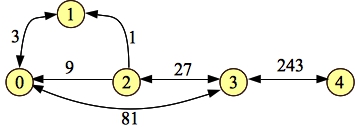And the final path: 0-3-4:

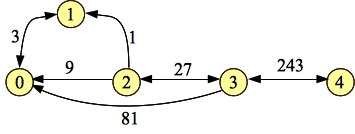We're done. As before, go ahead and compare the final residual above to this one -- you should see how they match. Because the two graphs have the same structure, we can use either of them to find the minimum cut in the original graph. So, by using the second version, which required no addition and subtraction, we end up with a residual graph that we can use to find the minimum cut in the original graph, and the sum of the edges in the minimum cut equals the maximum flow!

We really should do a formal proof of this, but I'm not going to -- I'll leave that to the motivated student. When we program it, what we'll do is represent each edge's weight by its logarithm base three (which is just its index in the input vector). That will be a number between 0 and 1999. No more worries about long long's!

We can use the Edmonds-Karp algorithm to find augmenting paths, and then when we process the residual graph, we don't bother adding small values to big values, or subtracting small values from big values. We simply use the big values.

When we're done, and we can no longer find any augmenting paths, then we use the residual to find the minimum cut in the original graph. The sum of those edges is our answer!

Let's go ahead and do final example from the problem specification to help reinforce. This is example 4. Here's the graph where edge weights are represented by their logarithms base three:

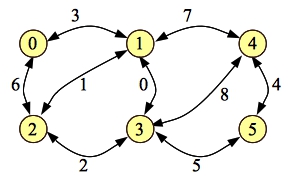If we use Edmonds-Karp, there are three paths that we can choose first (with three edges). Let's do 0-1-4-5. Our residual simply removes the forward edge [0-1]:

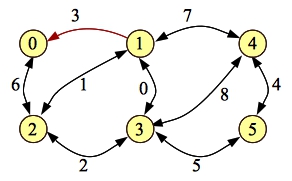Next, we have 0-2-3-5. The residual simply removes the forward edge [2-3]:

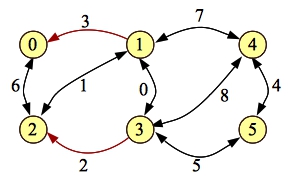The shortest hop path on the graph is now 0-2-1-3-5. To process the residual, we remove the edge [1-3]:

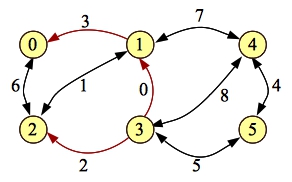There are still a few paths through the graph. The shortest hop one is 0-2-1-4-5 whose limiting edge is [2-1]:

Now there are no augmenting paths through the graph. We perform the DFS to find nodes reachable from the source in the final residual graph. Those are nodes 0 and 2. Our minimum cut is then the edges in the original graph that go from 0 or 2 to any other nodes. Those are edges [0-1], [2-1] and [2-3]. Their weights are 3, 9 and 27, so our final answer is 39 (which matches the correct one).

You should note that we had to use the minimum cut to find our answer. Were we to have used our flow calculations processing the augmenting paths, we would have come up with an incorrect answer of 40. Why? Because we added one unit of flow when we processed 0-2-1-3-5, and then three units when we processed 0-2-1-4-5; however, in reality, that last path only added two units of flow. We ignored this fact, because the residual graphs that remained were the same as the correct residual, and that means that we could use it to calculate the correct minimum cut, even though we calculated the incorrect flow. That's pretty cool, isn't it?

#2: Partitions with benefits: SRM 653, D1, 450-pointer - Singing

Let me give a pithier explanation. This topcoder problem is one of a class of problems that don't look like maximum flow problems, but indeed are. These problems follow a pattern:

You have a collection of elements, and weights on various pairs of elements. And two special elements, A and B. Your job is to partition the elements into two sets such that:
  • Element A is in one set, and element B is in the other.
  • You can only include the weight between two elements if they are in the same partition.
  • Your job is to determine a way to partition the elements to either maximize the weights that are included, or minimize the weights that are not included.
This problem may be solved with network flow.

Let's try an example that has a topcoder-esque flavor.

In ancient times, there was a Norse kingdom inhabited by six people: Thor, his wife Sif, his mistress Jarnsaxa, and random commonfolk Sven, Astrid and Bjorn. Each pair of people has hidden a certain amount of gold in special hiding places: 

- Thor     and Sif      have hidden 1000 pounds of gold together.
- Thor     and Astrid   have hidden   15 pounds of gold together.
- Sif      and Astrid   have hidden    4 pounds of gold together.
- Astrid   and Sven     have hidden    7 pounds of gold together.
- Thor     and Sven     have hidden   12 pounds of gold together.
- Astrid   and Jarnsaxa have hidden    3 pounds of gold together.
- Sif      and Jarnsaxa have hidden    8 pounds of gold together.
- Sven     and Bjorn    have hidden    2 pounds of gold together.
- Jarnsaxa and Bjorn    have hidden    9 pounds of gold together.
The hiding places are defined by MD5 hashes (kind of like the Plank Random Choosing Algorithm), and as such, if two people have hidden gold together, neither can retrieve it without the help of the other.

Sif has discovered Thor's misgivings with Jarnsaxa, and she is going to leave him and start her own kingdom with any of the people who want to join her. Thor will remain with the others. In any case, people in the same kingdom will retrieve and split their gold. People in different kingdoms will say goodbye to their gold forever.

The remaining four people (Jarnsaxa, Sven, Astrid and Bjorn) have to decide what to do. They are rational, so they decide that they will choose kingdoms so as to maximize the amount of gold that is retrieved.

To which kingdoms does everyone go?

This fits the above description exactly. The "weight" between two elements is the amount of gold in their shared safety deposit boxes, and the partitioning is done by the two kingdoms.

To solve this type of problem, you turn it into a graph, with elements of the population as nodes, and weights as edges. You then define a source A and a sink B, and find the minimum cut in the graph. Those are the edges excluded. The other edges are the ones included, and by determining the minimum cut, you have maximized the edges that are included.

Let's do an example with the above problem. The answer becomes pretty obvious when you create a graph from the problem:

With Thor as a source and Sif as a sink, it's pretty easy to see that the maximum flow is 1009, and that the minimum cut is composed of the red edges. Sven and Astrid stay with Thor. Bjorn goes with Sif, and in a fit of irony, Jarnsaxa goes with Sif as well...

Armed with this information, let's take a look at the Topcoder problem. I'll summarize it below in terms of numbers and sets. You are given four input values: The numbers N, Low and High and a vector P of numbers between 1 and N.

You are going to partition the numbers from 1 to N into two sets, A (for Alice) and B (for Bob). The numbers from 1 to Low-1 must go into set B and the numbers from High+1 to N must go into set A. The numbers from Low to High can go into either set.

You want to assign the numbers so that the number of adjacent numbers in the vector P that belong to different sets is minimized.

Let's take example three from the Topcoder problem. In this example, N is 10, Low is 4, and High is 5. The vector P is {1, 4, 3, 5, 2, 5, 7, 5, 9}. The only unassigned numbers are four and five. We can enumerate their potential assignments, and we'll see that the smallest number of adjacent numbers in different sets is three:

Of course, N, Low and High can range up to 1000, so an enumeration solution isn't going to work in general, but it should help you read the problem.

Now, suppose we want to turn this into a partitioning problem like Thortopia above. Obviously, the elements that we are partitioning are the numbers, and some of them are going to be assigned to sets unconditionally (the low and high numbers). We associate an edge between two numbers if they are adjacent in P, and the weight we associate with the edge is the number of times that they are adjacent in P. We want to partition the numbers and minimize the weights of the edges that span partitions. Voila -- problem solved -- this fits our paradigm exactly!

There is a slight issue with how we handle the numbers from 1 to Low-1, and from High+1 to N. One very simple way is to change P so that all numbers from 1 to Low-1 are replaced with the number 0, and all numbers from High+1 to N are replaced with N+1. Example 3 would have P become: { 0,4,0,5,0,5,11,5,11 }. Then, the nodes 0 and N+1 will be the source and sink in our graph calcaultion. Here's the graph for example 3:

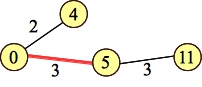It's pretty easy to see that the maximum flow from 0 to 11 is 3, as is the minimum cut. Hence the answer of 3.

I'm going to describe another way of handling the low and high numbers, because it's good for you to see this trick. We're going to have a source node labeled B and a sink node labeled A. We don't modify P, but leave all of the numbers as they are. And we add weights of infinite size between all low numbers and B, and between all high numbers and A. Do you see how that forces the low numbers into B and the high numbers into A? Here's the new graph for example 3:

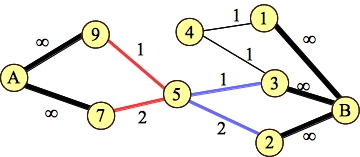It's pretty clear that the maximum flow through this graph is three, and the minimum cut is either the two red edges or the two blue edges.

Just for yucks, here's the graph for example 4, with the cut edges colored red. (Unlabeled edges have weights of one).

In class, we go through this "clicker" question, which is really too hard to be a clicker question. Here's how to use vi and shell scripting to get the answer.

A digression into minimum cuts and infinte edges.

I find the two problems below very difficult to think about, so let's develop a little theory.

Observation #0: If there is augmenting path in the original graph, then one of the edges in the path is in the minimum cut. I don't even need to prove this, because it's pretty obvious, but I'll use this observation later.

Observation #1: If there is an augmenting path in the original graph, then there cannot be two edges from that path in the minimum cut

We can prove this by contradiction. Let's call the edges (a,b) and (c,d). Let's assume that both edges are in the minimum cut. Then, by the definition of the minimum cut, in the final residual graph, there is a path from S to a, and a a path from S to c; however, there is no path from S to b or S to d. Let's illustrate that:


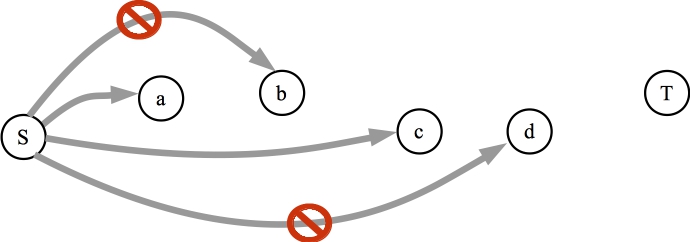The residual graph. We know this is true because (a,b) and (c,d) are in the minimum cut.

We can create the residual graph from the flow graph. In particular, the residual graph equals the original graph with the following modifications. If edge (e,f) is in the flow graph with a flow of x, then x is subtracted from (e,f) in the residual graph, and added to (f,e). Our assumption is that there is a flow graph with a path from S to T through both (a,b) and (c,d). We draw that as follows:


The flow graph.

This means that the following edges/paths are in the residual graph:


The residual graph. We know these edges/paths have to be in the residual graph.

If we combine the edges from our two residual graphs, we see a contradiction:


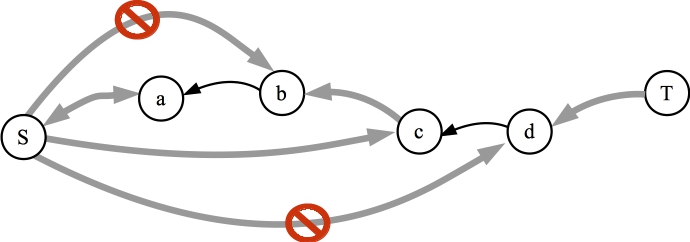The residual graph. There is a contradiction here, because there is a path to b, but there cannot be a path to b.

You can combine observations 0 and 1 into the following: If there is an augmenting path in the original graph, then exactly one of its edges will be in the minimum cut.

Observation #2: If there is an edge of infinite capacity from node a to node b then if a is on the source side of the cut, meaning a is reachable from the source in the final residual graph, then b must also be on the source side of the cut.

Let's highlight this observation with a picture:


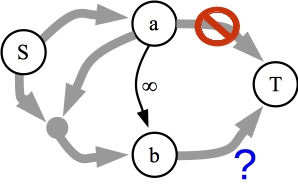The residual graph. Since a is on the source side of the cut, there is a path from S to a and no path from a to T. The question is, whether the edge with infinite capacity from a to b forces b to be on the source side of the cut too.

This one is pretty clear -- the infinite capacity edge means that there is a path from S to b, so there can't be a path from b to T:

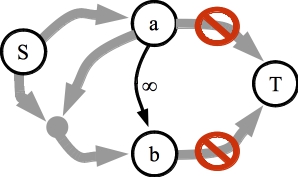
Observation #2, done.

Oh, and Observation #3 isn't necessary for anything, but it is an interesting observation, so I'll keep it here.

Observation #3: If there is an edge of infinite capacity from node a to node b, and if a is on the non-source side of the cut, and if you can construct a maximum flow graph that has flow going through the edge, then then b will be on the non-source side.

This is a tricky observation, in my opinion. Here's a picture of the observation:


The residual graph. Since a is not on the source side of the cut, there is no path from S to a. The question is, that if we can construct a maximum flow graph that uses the infinite capacity edge, can there be a path from S to b?

The proof is like observation #1: Since we can have flow across the infinite edge, the residual graph will have an edge from b to a. That means that if there is a path from S to b, then there is a path from S to a. Contradiction. Boom:

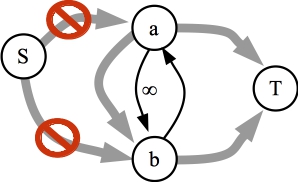
I want to give two example graphs to illustrate why (at least to me) this is tricky. Below is a graph where a is not on the source side of the cut. We can clearly construct a maximum flow graph that uses the edge (a,b), so b must be on the non-source side as well. It is.

On the flip side, in the graph below, it is impossible to construct a maximum flow graph that uses the edge (a,b). In order to push 9 units of flow through, all of the flow through a has to go directly to T. As you'll note, b is on the source side of the cut.

#3: More partitions with benefits: SRM 634, D1, 500-pointer - SegmentDrawing

A more general problem

You have two distinct sets of items, A and B. Each item in the two sets has a positive weight, and you want to select a collection of items from the two sets that maximizes their weight, subject to constraints of a particular form.

The constraints are of the form: "If you choose this item from set A, then you can't choose these items from set B," and, conversely, "If you choose this item from set B, then you can't choose these items from set A."

You may solve this problem with network flow.

One way to solve this problem is to model it as a graph for network flow. There is a source A and a sink B, and nodes for every element in each set. The elements in set A have edges from node A with weights equal to their weight, and the elements in set B have edges to node B with weights equal to their weight. Finally, for every constraint involving an item in set A and and item in set B, there is an edge of infinite capacity from the node from set A to the node from set B.

Now, determine the minimum cut of the graph. It will have to involve only edges from A or to B. The nodes corresponding to those edges are not in our optimal set. The remaining nodes are.

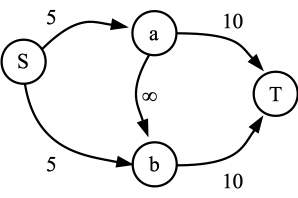
Does this work? Let's try a simple example. Suppose A = { c, d, e } and B = { f, g, h }, and weights are assigned as follows:

(c=16, d=5, e=4, f=8, g=7, h=11)

Suppose I want to choose a collection of elements from these sets such that the collection has maximum weight, but there are no constraints. Obviously, I just choose every element. However, I can model that as a graph as described above, with no edges from the A nodes to the B nodes:

It should be clear that there is no flow from A to B, so the minimum cut is composed of the empty set. Therefore, my collection is composed of all of the nodes.

Let's try a harder example. We'll use the same sets and weights as above, but now let's constrain it so that if you include any node from A, then you can't include any node from B. Again, we don't need network flow to solve this -- simply sum up the weights from A and the weights from B, and whichever is larger, you use all of them. But we can model it with a graph defined as above, where all of those thick edges have infinite capacity:

Here's the flow graph, with the edges on the minimum cut colored green.

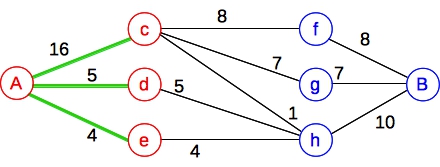This means that the elements of A are excluded, and our collection is composed of all of the elements of B: { f, g, h }. Of course, those three items have a greater sum than the elements of A.

Now, let's look another example, which is slightly more interesting. Let's suppose that:

Again, you don't need network flow to solve this. Simply take the greater of each pair: c, g and h. However, we can model it as a graph:

It should be clear that the max flow through this graph has three paths of flow 8, 5 and 4. Therefore, the min cut is composed of the green edges: (A,d),(A,e),(f,B), meaning those three nodes (d,e,f) are not in our collection. The other three (c,g,h) are. Nice.

And an even more interesting example. Let's add three more constraints to the last example:

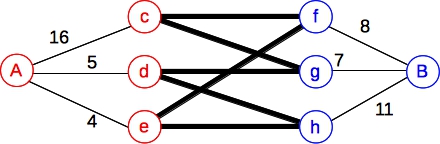Now it's not so simple to eyeball the weights and constraints. However, the graph will help us:

Here's the flow graph. I've drawn the min-cut edges in green:

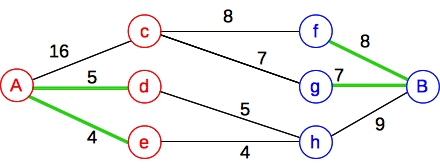That means that our collection consists only of the nodes c and h. As it turns out, that is the correct answer.

Can we prove that this is the best answer? Yes. Let's consider the constraints and the minimum cut. Each constraint represents a path through the graph with positive flow. This path has three edges -- one from A, the infinite capacity one, and the one two B. The combination of observations 0 and 1 says that the minimum cut will have exactly one of these edges, and of course it won't be the infinite capacity edge. So for each constraint, exactly one of the nodes will be included and one of them will not.

Now, let's look at the non-infinite edges that are not in the minimum cut. For each constraint, there is exactly one edge in this set as well. Therefore, those edges don't violate the constraints either. Since the minimum cut is the minimum set that doesn't violate the constraints, the other edges maximize the set that doesn't violate the constraints. Neat, no?

SegmentDrawing

Armed with this information, we can solve the Topcoder problem, which I summarize as follows: You have N points on a plane, each with specified (x,y) values. You are going to partition the points into two sets, Red and Blue to solve a maximization problem. Each pair of points has two score values -- RedScore and BlueScore. You score RedScore(a,b) when two points a and b are both in the Red set, and you connect them with a line segment. Similarly, you score BlueScore(a,b) when two points a and b are both in the Blue set, and you connect them with a line segment. There is a final constraint -- line segments from different sets cannot intersect (or share points). The input guarantees that no three points are co-linear.

Let's illustrate this with Example zero, which has four points: (0,1), (1,0), (0,-1) and (-1,0). I'll draw them on a graph and label their scores as colored edges:

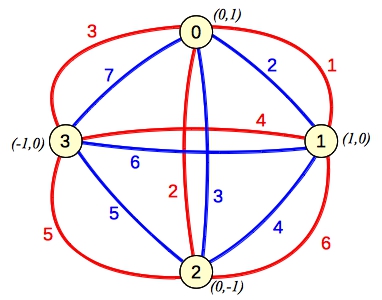The solution here is pretty easy -- simply color all of the points blue, and you get to sum up all of the blue edges: 27. The solution also helps you think about the problem. How can you partition the points into two sets legally so that you get to count scores from each set? Well, if I color points 0 and 1 red, and I want to include a blue score, I'll have to color points 2 and 3 blue. The only scores I would keep are the red score for (0-1), and the blue score for (2-3). The following input would yield that solution:

Let's call that "Example -1", since that is not an example from the topcoder specification, but we'll be referring to it later.

Now, let's formulate the problem in terms of the partitioning problem above. Given a set with N points, there are going to be exactly (N)(N-1)/2 red edges and (N)(N-1)/2 blue edges. These edges are going to be the elements that we partition in our general problem. You'll note, each edge has a weight. And we are selecting edges from each partition subject to the constraint that no edges from different partitions intersect. And we want to maximize the total weight of the selected edges.

Below, I'm redrawing the graph from Examples 0 and -1, but I'm simply labeling the edges, and not drawing the weights:

Suppose you select red edge 01 to be in your set. Then it should be clear that you cannot select blue edges 01, 02, 03, 12 and 13. However, you can select edge 23. On the other hand, if you select red edge 02, then you can't select any blue edge.

Every edge has constraints on the edges from the other set. Specifically, red edge AB excludes every blue edge with endpoints A or B, and every blue edge that intersects AB.

We now know enough to use the the network flow technique from the above general problem formulation to solve the problem. Here's the network flow graph for Example 0:

(The black edges have infinite capacity).

It isn't easy to figure out the flow here, but it ends up saturating all of the red edges, which means that they compose the minimum cut, and our answer is the sum of all of the blue edges. In some respects Example -1 is easier to see. The graph has the same structure as example 0, but different weights:

You can process augmenting paths by always including the edges with weight 100 -- eventually the flow will saturate all of the other edges, yielding a maximum flow of (3+1+5+6+4)+(3+7+2+5+4) = 41. The minimum cut will be composed of the saturated edges, and the answer will be the sum of the remaining edges: 200.

I'm afraid that the other examples will be too complex to draw; however, I'm hoping that the above examples have helped you figure out how to code up the solution!

#4: I'm glad no one put a gun to my head to solve this problem: SRM 633, D1, 600-pointer - DoubleTree

This is a hard problem. My attempt was to solve it with Dynamic Programming, which I did, but it choked on the larger problems. I looked up the solution online, and let's just say, it took a while for me to understand it. I'm glad my livelihood did not depend on coming up with the solution to this problem.

As with the problems above, there's a more general problem that seems quite unrelated to network flow that you can solve with network flow. Actually, in this case, the general problem seems unrelated to the Topcoder problem! We'll get to that. The problem is this:

You have a collection of elements with weights, which may be positive or negative numbers. You want to choose a subset of these elements such that their total weight is maximized.

There are constraints to make your life difficult, which are of the form, "If you include element X in your subset, then you must include element Y too." Let's abbreviate that X → Y.

This problem may be solved with network flow.

As always, an example or two never hurts, so let's do a few:

Example 4A
Element 0: Weight = 50
Element 1: Weight = -100
Example 4B
Element 0: Weight = 50
Element 1: Weight = -100
0 → 1
Example 4C
Element 0: Weight = 100
Element 1: Weight = -50
0 → 1
Answer: { 0 } Answer: { } Answer: { 0, 1 }

The conversion to network flow is a little confusing. First, choose a number bigger than the maximum positive value. Call that number B. You are going to have a source node S and a sink node T, plus a node for every element in the set.

You have an edge from S to each node, whose weight is B, and you have an edge from each node to T, whose weight is B-weight. For each constraint of the form X → Y, you will have an edge from X to Y with infinite weight.

Determine the maximum flow from S to T, and the minimum cut of the graph. If an edge of the form (X,T) is in the minimum cut, then X should be included in the subset that answers the problem. Moreover, the weight of that subset will be NB - Flow, where N is the number of elements in the set.

Let's explore how this works. First, take a look at the graph for example 4A:

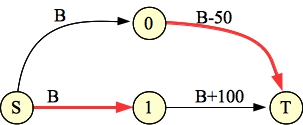I've colored the nodes that are in the minimum cut red.

It should be clear that there is an augmenting path through each element's node. The flow through that path is B, if the element's weight is negative, and B-weight if the element's weight is positive. That means that if element X's weight is negative, the edge (S,X) is in the minimum cut, and if it is positive, then (X,T) is in the minimum cut. That's exactly right.

The flow of the graph is going to be NB - (sum of positive weights). If you subtract that from NB, then you get the sum of the positive weights. Nice.

Adding a constraint makes it a little harder. Here are the two graphs for examples 4B and 4C:

4B
 4C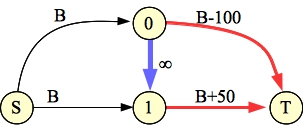

Can we prove that it works? Well, kinda, but it would probably take a real proof to be totally sure. There are a few things that are pretty clear:

The part of this which I haven't convinced myself is really true is that the maximum flow is indeed the maximum answer to this problem. I think that will take induction, and I do not want to do it. Just assume it's true.....

The Topcoder Problem

Back to the Topcoder Problem.

The problem is as follows. You have two trees with N nodes. Each node i has a weight w[i], which is the same in both trees. The weight can be negative. Your job is to find a subset of nodes, such that the subset is connected in both trees, and the sum of the weights of the nodes is maximized.

Let's look at an example (example 0 in the topcoder problem):

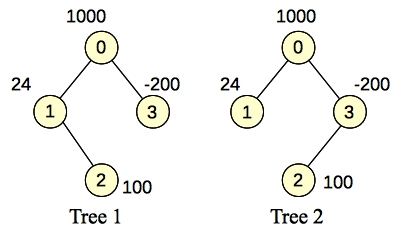You can eyeball that one to see that the subtree is composed of nodes 0 and 1. That is a connected component in both trees and its total weight is 1024. You'd like to be able to add node 2 to the mix, but if you do so, you'll have to include node 3, to make the component connected in tree 2. Because node 3's weight is -100, and node 2's weight is only 100, it is not profitable to add both nodes to our final set.

If you change node 2's weight to 200 and node 3's to -100, now your best set is all of the nodes. The total weight is 1124:

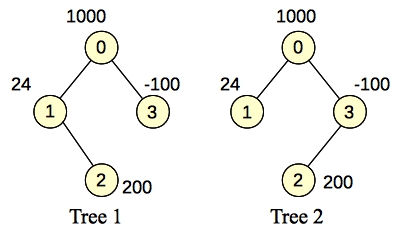How does this map to our set inclusion problem? First, we are going to solve the problem N times. Each time, we are going to affix a different node to be a root node of the tree, and find the largest connected subtree of both trees that have that node be the root. We'll select the best of these.

Now, given a root node, each non-root node has a parent in each of the trees. It may be the same parent (like nodes 1 and 3 above, which have node 0 as their parent when it is the root) or a different parent (like node 2). If a node is going to be in the connected subtree, then its parent (or parents) also have to be in the subtree. See how that fits the set inclusion problem?

Let me illustrate with example 0. Here, the set is composed of elements 0, 1, 2 and 3, with weights 1000, 24, 100 and -200 respectively. Plus, we have the following constraints:

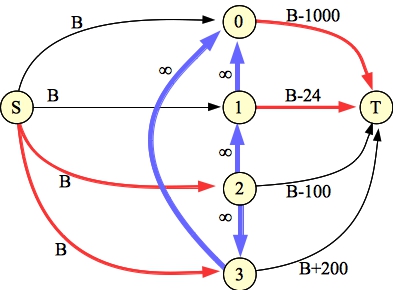So, we get the following graph, whose minimum cut is labeled in red. That corresponds to the answer, where nodes 0 and 1 are in the best subtree of both trees.

You'll note that the total flow is 4B-1024, so the total weight of the subset is 1024.

If you change node 2's weight to 100 and node 3's weight to -50, then you get the graph below, and you see that all four nodes are in the best subtree.

Now the flow is 4B-1124, so the total weight of the subset is 1124.

Tell me that's not a great problem.....