Question 1: 5 points

Grading

• Some of you said that although it only writes one file, it can read anything. Sure, that's true, but what is it going to do with that information if it can't communicate it to the evil source? I gave 2.5 points for that answer, since it was true, but incorrect.
• Some of you said that it doesn't test the user's code to see if it is malicious. That is equivalent to solving the halting problem and thus is impossible. We don't expect compilers to be able to do the impossible. 1 point for that answer.
• Some of you said that the code could easily have a buffer overflow attack without using gets() -- just make read/fread/fgets calls that use pointers that are too small. That's kind of reaching, I'd say, but not out of the realm of possibility, I guess. 3 points for that answer.

Question 2: 16 points

• Part 1: To calculate the maximum, assume that the code spans two pages (e.g. it starts at an address like 0x7f0), and the stack spans two pages. How about s? Well, if x = 2, it can span two pages. If x = 1026, it can span three. Extrapolating, that is floor((x-2)/1024))+2. So the answer is:
  Maximum = 6 + floor((x-2)/1024)).

  To calculate the minimum, assume that the code is all in one page, the stack is all in one page, and s starts on a page boundary.

  Minimum = 3 + floor((x-1)/1024)).

• Part 2: A working set with a window size of delta is the set of pages that are touched by any of the last delta instructions.

• Part 3: To calculate the maximum, suppose that s and e are on different pages. Moreover, suppose that L08 and L27 are on different pages. This means that four pages will be touched on every iteration of the loop. What about *s and *e? Well, first, assume that *s never equals *e. That means that on each iteration of the loop, 17 instructions are executed (L18-L20 are not executed). So, if delta equals 21K, you can perform 21/17 = 1.23K iterations of the loop. The exact value is not really important. What is important is that in 1.xK iterations, *s can touch three pages, as can *e. So the maximum is 10 pages.

  To calculate the minimum, now suppose s and e are on the same page, as are all of the instructions. If you execute all of the instructions in the loop, that will make 21/20K iterations -- still greater than 1K. However, now you can assume that only two pages are touched by *s and *e. Thus, the minimum is 6 pages.

• Part 4: Ok -- s starts on a page boundary, and e will start 36 bytes past a page boundary. Palcount starts on a page boundary, so all of its instructions are in one page, and since the fp is in the middle of a page, all the stack variables will be on one page. So, what's going to happen -- well, at every iteration, the stack and code pages are touched, as are the pages containing the current *s and *e. On the 37th iteration, and every 1024 iterations after that, *e will cross a page boundary. On the 1024th iteration and every 1024th iteration after that, *s will cross a page boundary. On the last iterations, *s and *e will be on the same page.

  Put another way, all of s spans 1025 pages. We touch the stack/code variables multiple times each iteration; however we only touch *s at L15 and *e at L13. Thus, with LRU, the code & stack will never be kicked out; only old *s and *e pages. Thus, you will have 1025 page faults -- one for every page of s.

• Part 5: With FIFO, here's what's going to happen:
  • The code & stack are in memory.
  • *e will fault in. Call it e_0.
  • *s will fault in. Call it s_0.
  • At iteration 37, a new e_1 will fault in.
  • At iteration 1K, a new s_1 will fault in.
  • At iteration 1K+37, a new e_2 will fault in, which will kick out a code or stack page.
  • Then the code/stack page will fault in, kicking out the other code/stack page.
  • Then the other code/stack page will fault in, kicking out e_0.
  • At iteration 2K, s_2 will fault in, conveniently kicking out s_0.
  • At iteration 2K+37, e_3 will fault in, conveniently kicking out e_1.
  • At iteration 3K, s_3 will fault in, conveniently kicking out s_1.
  • At iteration 3K+37, e_4 will fault in, kicking out a code/stack page.
  • Then the code/stack page will fault in, kicking out the other code/stack page.
  • Then the other code/stack page will fault in, kicking out e_2.
  • And so on.

  So, we will still have the 1025 page faults for every page of s. Additionally, we will have two page faults every time e_x is faulted in (x is even and greater than zero), because it will kick out a code/stack page. There are 1025 total pages. e_0 will be page #1024 (zero indexed). e_2 will be page #1022. The last e_x will be page #512. So, there are 256 even and positive values of x, resulting in 512 additional page faults. So - the total number of page faults is 1025+512 = 1537.

• Part 6: This algorithm was mentioned in class and is in the book. Suppose we always keep a free frame pool of two pages, and when we free a frame, we maintain its identity. Then when a stack/code page gets evicted, it goes on the free frame list, but does not get overwritten. Then when it faults back in, it is sitting there on the free frame list, and does not cost any disk I/O. In this way you'll still have 1537 page faults, but only 1025 disk reads.

Grading

• Part 1: 3 points. If you used division, I assumed that it was integer division.
• Part 2: 2 points.
• Part 3: 3 points.
• Part 4: 2 points.
• Part 5: 3 points.
• Part 6: 3 points.

Question 3: 11 points

• Part 1 - 1 point: 0x100 - 0x2ff.
• Part 2 - 1 point: 0x400 - 0x6ff.
• Part 3 - 1 point: 0xfffb00 - 0xfffeff.
• Part 4 - 1 point: Ok -- the address space is 0x1000000 bytes. That makes 0x1000000 / 0x100 = 0x10000 = 64K. A single level page table will have to have 64K entries. A page can hold 256/4 = 64 PTE's, so RedHat will have to have 64K/64 = 1024 pages of PTE's.
• Part 5 - 3 points:
  
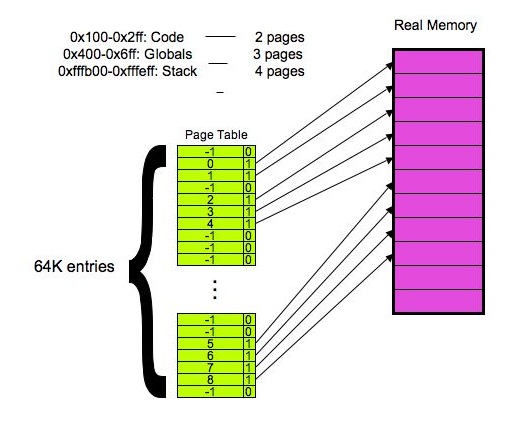
• Part 6 - 1 point: 18 pages -- 2 inner and 16 outer.
• Part 7 - 3 points:
  

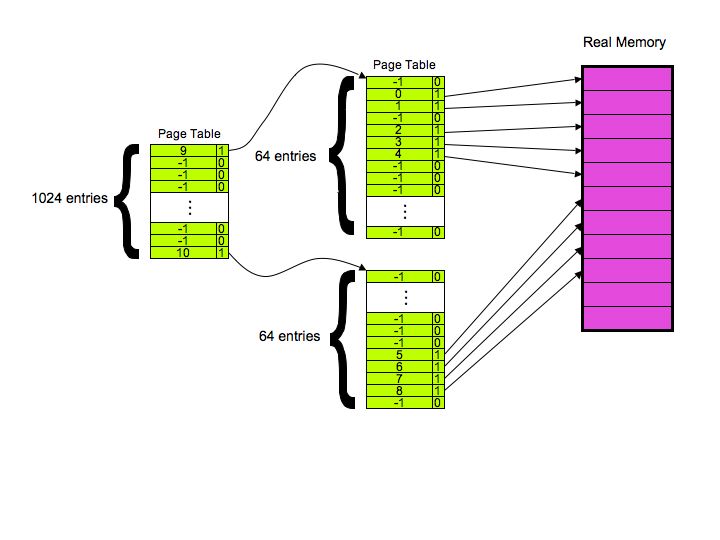
Question 4: 6 points

"For example, the first link in the first link block contains the link for the first data block on the list. Thus, if a file is composed of multiple blocks, the link for the file's first data block points to the second data block, and so on. Obviously, the last block's link will contain a NULL pointer.

"This scheme is preferable to storing links in the data blocks for two main reasons. First, the block's size can be a power of two, which is often very convenient. In other words, the block itself is not broken up into a data portion and a metadata portion. Second, the link blocks themselves may be cached in the operating system, and therefore finding the bytes in the middle of a file does not require reading all of the previous data blocks from disk. Instead, the cached links may be used without any extra reading of data from disk.

"The links also provide a nice way to identify free blocks -- instead of having a NULL pointer or a pointer to another block, the link can have a different sentinel value that flags it as a free block.

"There are two kinds of caching in this system. The first is caching the link blocks, as discussed above. The second is performing standard disk block caching -- either LRU caching for frequently used blocks, or lookahead caching to optimize the performance of serial file access."

Grading

• Variant of linked allocation scheme: 1 points
• Each file's "metadata" is a pointer to the first block: 1 point
• All the links held in one set of blocks on disk; the rest have data: 1 points
• Link for block i is in pointer i.
• Can cache the index blocks to reduce disk overhead on random access : 1 points
• Can have standard read caching for sequential access: 1 point