TCO 2008 Q2 1000-pointer (BlackWhiteRectangles)

James S. Plank

Mon Nov 4 13:21:14 EST 2013.
Latest modification: Thu Sep 22 13:40:25 EDT 2016

Problem Statement.
A main() with the examples compiled in.
A skeleton that compiles with main.cpp.
gen_input.cpp -- used by tests.sh.
tests.sh. MD5 hash: f244fe896aad24a927907766877e7dde
answers.txt. MD5 hash: 671f508e9741ad83242d876ce67e9309
Problem Given in Topcoder: 2008
Competitors who opened the problem: 1086
Competitors who submitted a solution: 148
Number of correct solutions: 62
Accuracy (percentage correct vs those who opened): 5.7%
Accuracy (percentage correct vs those who submitted): 41.9
Average Correct Time: 46 minutes, 26 seconds.

If Topcoder's Servers are Down

Here is a summary of the problem:

You are dealing with the cartesian coordinate system from (0,0) to (40000,40000).
You will be given a collection of rectangles, specified as (x₁, y₁, x₂, y₂, type).
For each of (x₁, y₁) is the lower left corner, and (x₂, y₂) is the upper right corner.
Each of these rectangles contains (x₂-x₁)*(y₂-y₁) 1x1 squares. Initially in the entire coordinate system, all 1x1 squares are colored white.
Each rectangle will (potentially) color some squares black. How it does so, depends on the type, where the lower left corner of each of these pictures goes at (x₁, y₁), and the patterns repeat to fill the rectangle.

Type 1
Type 2
Type 3
Type 4
The rectangles are given as a vector of strings, where each string contains x₁, y₁, x₂, y₂, and type separated by spaces.
In the specifications, x₂ will be greater than x₁, and y₂ will be greater than y₁.
All of the x and y values will be between 0 and 40,000.
Return the number of black squares.

Examples

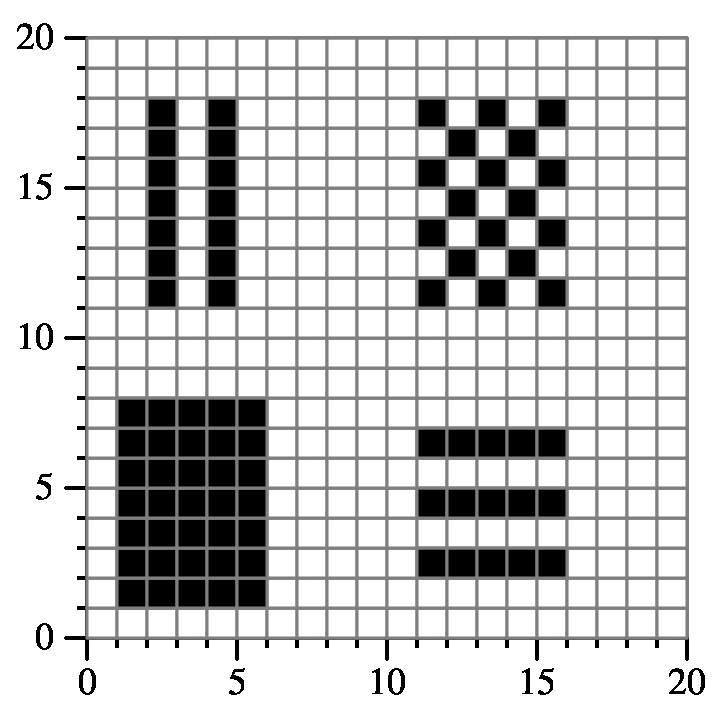
Example 0:
  {"1 1 6 8 1",
   "11 1 16 8 2",
   "1 11 6 18 3",
   "11 11 16 18 4"}
Returns: 82

Here is a drawing of the relevant part of the grid:

Example 1:
{"1 1 11 11 1",
 "1 1 11 11 2",
 "9 9 19 19 3",
 "9 9 19 19 4"} 
Returns: 172

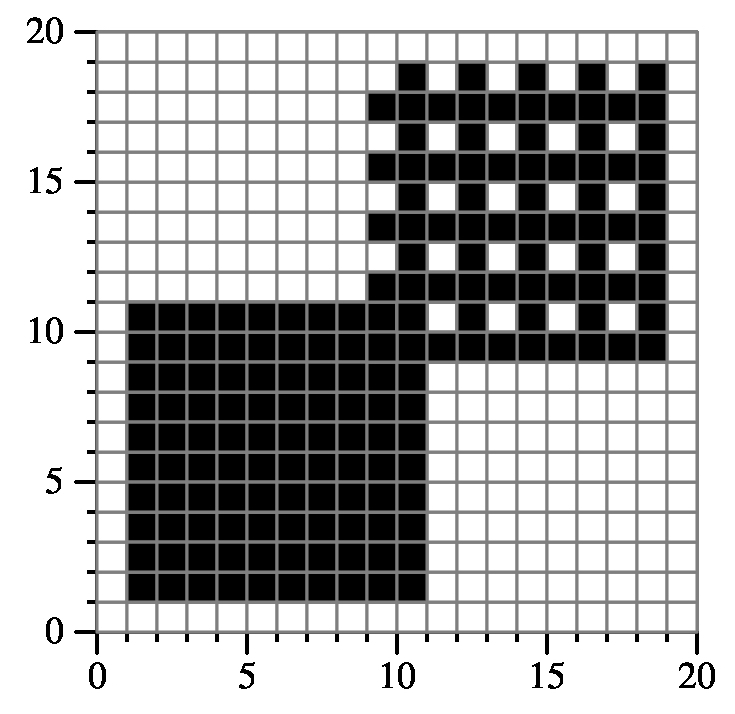Example 2:
{"1 6 9 9 1"
 "1 9 7 10 1",
 "1 5 8 7 1",
 "2 6 8 8 1",
 "2 1 3 4 1"}
Returns: 40

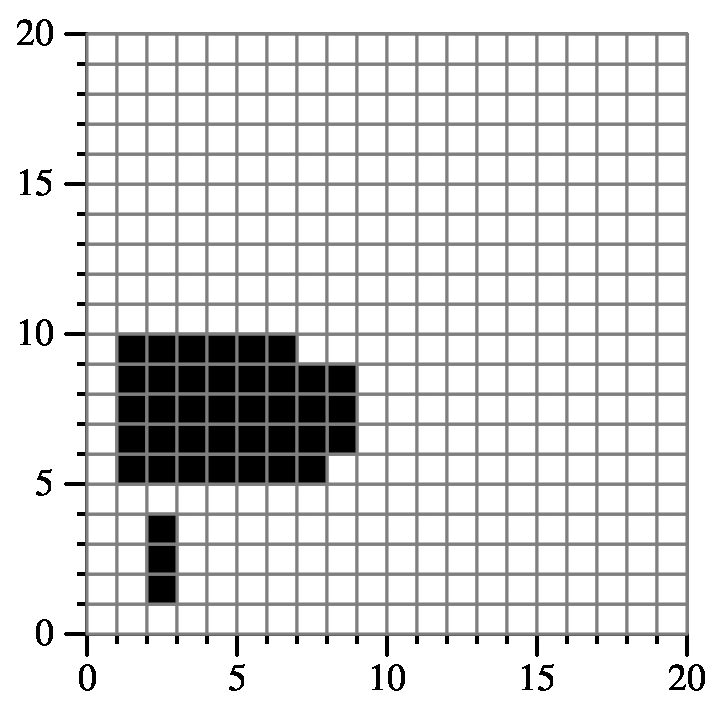Example 3:
{"7 5 9 6 4",
 "6 3 9 6 4",
 "8 3 9 8 4",
 "5 9 10 10 4",
 "5 3 8 5 4"}
Returns: 13

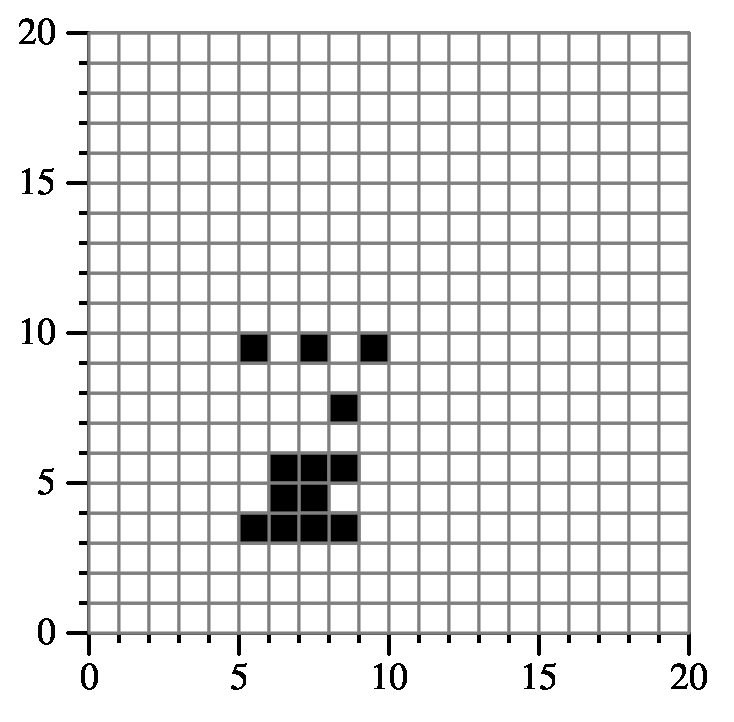Example 4:
{"7 1 10 3 1",
 "8 2 9 7 4",
 "5 3 7 4 3",
 "4 3 9 4 2",
 "3 1 9 2 1"}
Returns: 13

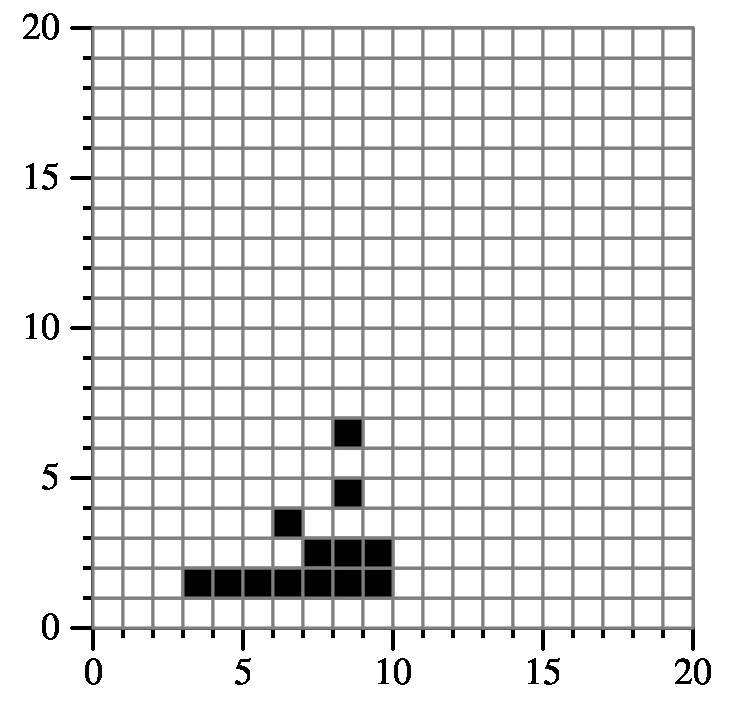Example 5:
{ "1  12  7 16  3",
   2  10  7 13  3",
   2   2 10 11  4" };
Returns: 54

tests.sh and answers.txt

tests.sh uses the program gen_input. You can compile it with the makefile. When you run it, the output should be identical to answers.txt.

Hints

This one is fun. Let me give you the general outline. You can't simulate the process directly because the constraints are too large. Instead, you should break up the region into smaller rectangles, where each rectangle has the same patterns applied to it. You then note which patterns are applied to the rectangles, and calculate the number of black squares in each rectangle. Sum them up and you're done.

I'll give an example here, which is example 5 above:

{ "1  12  7 16  3",
   2  10  7 13  3",
   2   2 10 11  4" };

This results in the following grid -- I've drawn the outlines of the three rectangles in different colors:

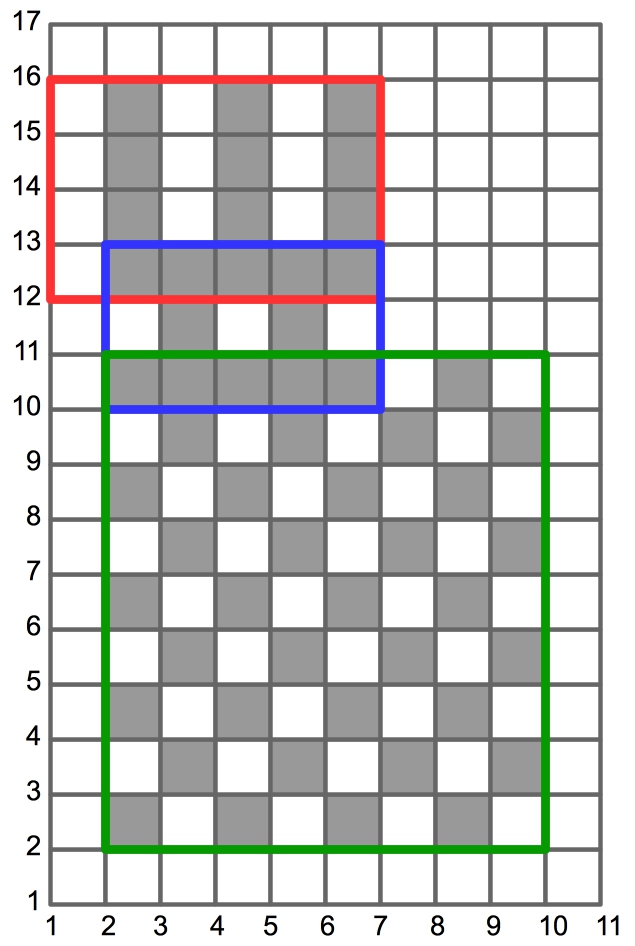Now, what I did was split up my grid into rectangles. Order all of the x1's and x2's, and all of the y1's and y2's:

X's: { 1, 2, 7, 10 }
Y's: { 2, 10, 11, 12, 13, 16 }

For each consecutive pair of X's and Y's, there is a rectangle defined that has had the exact same patterns applied to it. Your job is to split up the grid into these rectangles, and identify the pattern applied to it. I'm going to do that pictorally below:

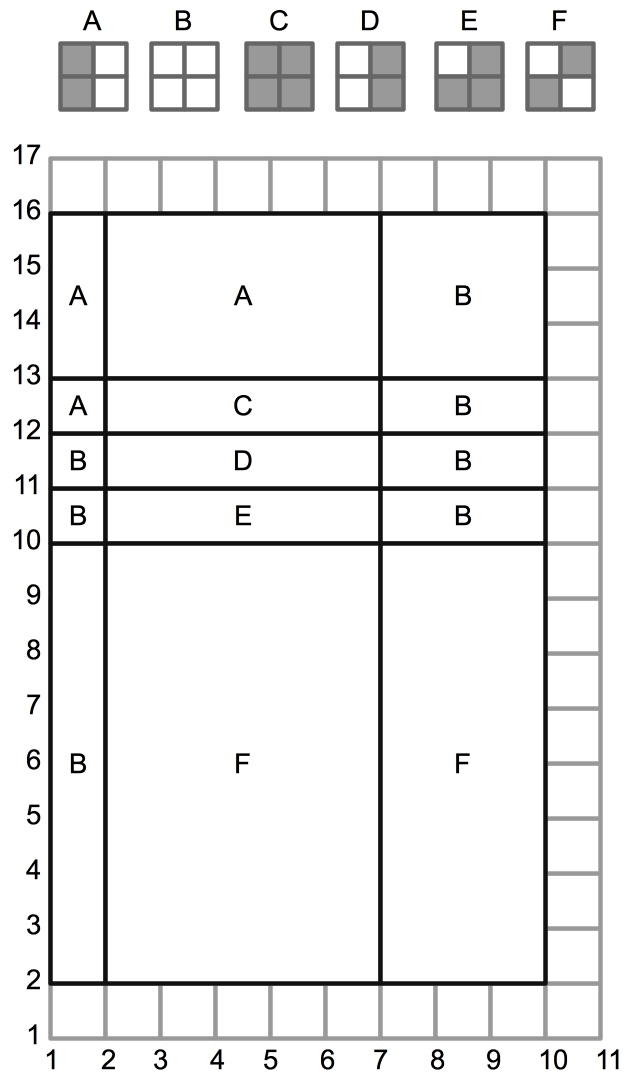The way I identified patterns was as 2x2 grids, which represent how each rectangle is colored, as long as the grid starts on an even row and column. For example, pattern "A" is used when a rectangle has all of the even columns black and odd columns white. Pattern "D" has all of the even columns white and the odd columns black.

Once you have your grid broken into rectangles, and you have identified the patter for each rectangle, then you determine how many black squares are set in each rectangle. That takes a little effort, because you have to consider whether the starting rows/columns are even or odd, and whether the width/height is even or odd.

In this example, the upper-left rectangle will be counted as having zero black squares, because it is pattern "A", but it starts on an odd column. The rectangle to its right will add 9 black squares, because it is a 5x3 rectangle of pattern "A", starting on an even column (yes, it starts on an odd row too, but that doesn't matter in this case).

I used bit arithmetic and single ints to hold the patterns. You may want to give that some thought, as I found it was easier.

Good luck -- this one is fun, but takes some attention to detail.

More Help

Here's a little more help, in case the above explanation is leaving you wanting. All of this is with respect to the example above. The first thing that I did was define all of the rectangles, in terms of their lower-left positions, widths and heights:

X	Y	Width	Height
1	2	1	8
1	10	1	1
1	11	1	1
1	12	1	1
1	13	1	3
2	2	5	8
2	10	5	1
2	11	5	1
2	12	5	1
2	13	5	3
7	2	3	8
7	10	3	1
7	11	3	1
7	12	3	1
7	13	3	3

I had a struct for each rectangle, which contained these fields, plus the "pattern". I stored the pattern as an int, and I only used the lower four bits of the int:

Lowest bit: lower left-hand bit of the pattern. This is the bit that is set in even rows and even columns.
Next bit: lower right-hand bit of the pattern. This is the bit that is set in even rows and odd columns.
Next bit: upper left-hand bit of the pattern. This is the bit that is set in odd rows and even columns.
Next bit: upper right-hand bit of the pattern. This is the bit that is set in odd rows and odd columns.

For example:

the pattern A above would be represented as 0x5.
The pattern B above would be represented as 0x0.
The pattern C above would be represented as 0xf.
The pattern D above would be represented as 0xa.
The pattern E above would be represented as 0xb.
The pattern F above would be represented as 0x9.

Next, I went through each input rectangle, and determined the pattern of the rectangle. You'll note that the pattern depends both on the "type" of the pattern, and on whether the starting row/column is even or odd. Let's process the first rectangle: [1, 12, 7, 16, 3]. In this pattern, the even numbered columns are block, so the pattern is pattern A, or 0x5. So, you go through each of the rectangles in your map that correspond to the first rectangle, and you can do a binary or of 0x5 with the patterns that are there already:

X	Y	Width	Height	0x0
1	2	1	8	0x0
1	10	1	1	0x0
1	11	1	1	0x0
1	12	1	1	0x5
1	13	1	3	0x5
2	2	5	8	0x0
2	10	5	1	0x0
2	11	5	1	0x0
2	12	5	1	0x5
2	13	5	3	0x5
7	2	3	8	0x0
7	10	3	1	0x0
7	11	3	1	0x0
7	12	3	1	0x0
7	13	3	3	0x0

Next, let's process the second rectangle: [2, 10, 7, 13, 3]. In this pattern, the odd numbered columns are block, so the pattern is pattern D, or 0xa. So, you go through each of the rectangles in your map that belong to the second rectangle, and you can do a binary or of 0xa with the patterns that are there already:

X	Y	Width	Height	0x0
1	2	1	8	0x0
1	10	1	1	0x0
1	11	1	1	0x0
1	12	1	1	0x5
1	13	1	3	0x5
2	2	5	8	0x0
2	10	5	1	0xa
2	11	5	1	0xa
2	12	5	1	0xf
2	13	5	3	0x5
7	2	3	8	0x0
7	10	3	1	0x0
7	11	3	1	0x0
7	12	3	1	0x0
7	13	3	3	0x0

Next, let's process the last rectangle: [2, 2, 10, 11, 4]. This is a checkerboard, where the lower-left and upper-right corners are set: Pattern F, which is 0x9. So, you go through each of the rectangles in your map that belong to the last rectangle, and you can do a binary or of 0x9 with the patterns that are there already:

X	Y	Width	Height	0x0
1	2	1	8	0x0
1	10	1	1	0x0
1	11	1	1	0x0
1	12	1	1	0x5
1	13	1	3	0x5
2	2	5	8	0x9
2	10	5	1	0xb
2	11	5	1	0xa
2	12	5	1	0xf
2	13	5	3	0x5
7	2	3	8	0x9
7	10	3	1	0x9
7	11	3	1	0x0
7	12	3	1	0x0
7	13	3	3	0x0

Now, for each rectangle, you have the following information:

X value of lower-left corner.
Y value of lower-left corner.
Width
Height
Pattern

For each rectangle, you can now determine how many black squares are set. Do this with a nested for loop:

for (i = 0; i < 2; i++) {
  for (j = 0; j < 2; j++) {
    If the cell corresponding to column i and row j in the pattern is set, then {
      Count the number of cells in the rectangle whith x%2 = i, and y%2 = j.
      Add these to the total sum.
    }
  }
}

For example, consider the rectangle [2, 2, 5, 8]:

When i=0 and j=0, the bit in the pattern (0x9) is set. You can count 3 even columns in the rectangle and 4 even rows, so add 12 black rectangles.
When i=0 and j=1, the bit in pattern 0x9 is not set.
When i=1 and j=0, the bit in pattern 0x9 is not set.
When i=1 and j=1, the bit in pattern 0x9 is. You can count 2 odd columns in the rectangle and 4 odd rows, so add 8 black rectangles.

I hope that helps you, if you're having trouble.

Smore more help if your program is too slow

This comes from a Piazza posting:

Matching created rectangles to input rectangles efficiently: In honors lab2, my program is correct but runs slow; I believe the reason why it runs slow is because of how I determine every input rectangle that each created rectangle corresponds to, needed to determine the patterns. I've written it in two completely different ways that work, but I can't figure out how to optimize this part. Is there an obvious solution I'm missing? Thanks.

James S. Plank: Do "sh -x tests.sh" and let me know the number of a test that is taking too long.

(Anon. Comp to classmates): Test 71 is one that takes longer than most others.

James S Plank 2: OK -- so there are 100 input rectangles. When you look at the unique x and y values here, there are 169 unique x values and 172 unique y values. That means you need to test 168*171 = 28728 rectangles. For each of these, you check it with the 100 input rectangles to see how many black squares there are. So:

Iterate x values (168)
  Iterate y values (171)
    Iterate input rectangles (100)
       Update number of black squares in the x/y rectangle: O(1)

There will be 2,872,800 iterations, each of which should be quick: O(1). This should take under a tenth of a second (my code is 0.076 seconds). I hope that helps.