TCO 2008 Q3 500-pointer (CableDonation)

TCO 2008 Q2 500-pointer (CableDonation)

James S. Plank

Sun Nov 24 18:53:42 EST 2013 Latest modification: Mon Apr 25 14:08:57 EDT 2022

Problem Statement.
A main() with the examples compiled in.
A skeleton that compiles with main.cpp.
gen_input.cpp -- used by tests.sh.
tests.sh.
answers.txt.
https://bitbucket.org/jimplank/plank-disjoint-sets - an open-source implementation of disjoint sets
Problem Given in Topcoder: 2008
Competitors who opened the problem: ?
Competitors who submitted a solution: ?
Number of correct solutions: ?
Accuracy (percentage correct vs those who opened): ?
Accuracy (percentage correct vs those who submitted): ?
Average Correct Time: ?

If Topcoder's Servers are Down

Here is a summary of the problem:

You have n rooms in your house.
You are given a vector C of n strings each of length n.
The character in C[i][j] represents a length of cable between rooms i and j. The character '0' means no cable. Characters 'a' through 'z' represent the numbers 1 through 26, and the characters 'A' through 'Z' represent the numbers 27 through 52.
There may be two cables connecting rooms i and j -- the entry in C[i][j] and the entry in C[j][i] (they may be different).
C[i][i] represents the length of cable that is entirely in room i.
You want to donate as much cable as you can to charity, yet still keep all of the rooms connected. Return the total length of cable that you can donate.
Return -1 if the rooms are disconnected from the start.
The Topcoder constraints are that the length of C is 50. However, the program gen_input.cpp increases these constraints to 500.

To test yourself, please do:

UNIX> g++ -o gen_input gen_input.cpp

Examples

#   C     Answer

0 "abc"   40 -- Donate everything but the cable of length 2 between 0 and 1
  "def"                           and the cable of length 3 between 0 and 2.
  "ghi"

1 "a0"    -1 -- The rooms are disconnected.
  "0b"

2 "0X00"  0 -- The rooms are connected, but there is no excess cable.
  "00Y0"
  "0000"
  "00Z0" 

3 "Az"    105
  "aZ"                            

4 "0top"  134
  "c0od"
  "er0o"
  "pen0"

Hints

It should be clear that this is a minimum spanning tree problem. The only subtleties are that you have to convert those letters to numbers, and then you have to discard unnecessary cables. Once you do that, you have to make sure that you create the proper undirected graph for Prim's algorithm.

Interestingly, if you use Kruskal's algorithm instead, you don't even have to discard cables or worry about direction. When you come upon a duplicate cable, or even a cable that goes from a node to itself, the algorithm won't consider it because the cable does not span disjoint sets. Think about that.

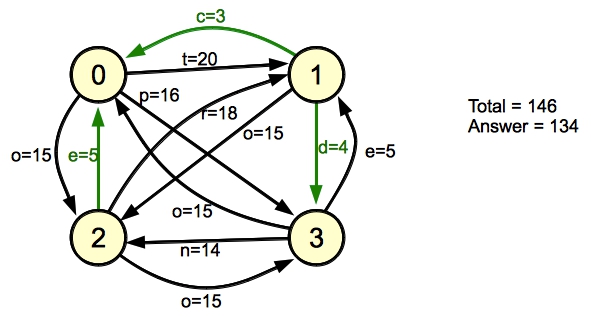
Let's see how it works on example 4, which is the most complex. Here's the graph:

You can see that if you use Kruskal's algorithm, it will process the edges in increasing order of size. It will process edge (1,0) first and (1,3) second. At that point, there will be two connected components: {0, 1, 3} and {2}. There are two edges of weight 5, so suppose it processes edge (3,1). It will see that this edge does not connect different sets, so it will ignore the edge. The next edge, (2, 0) does connect different sets. At that point, there is just one set, so we're done. The total cable donation is the total of all of the edges, which is 146, minus the edges in the minimum spanning tree, which is 12. The answer is 134.