SRM 470, D2, 1000-Pointer (ActivateGame)

James S. Plank

• Problem Statement.
• A main() with the examples compiled in.
• A skeleton that compiles with main.cpp.
• https://bitbucket.org/jimplank/plank-disjoint-sets - an open-source implementation of disjoint sets

• tests.sh.
• answers.txt.
• gen_input.cpp -- an input generator used by tests.sh

• Problem Given in Topcoder: May, 2010
• Competitors who opened the problem: 518
• Competitors who submitted a solution: 101
• Number of correct solutions: 62
• Accuracy (percentage correct vs those who opened): 12.0%
• Accuracy (percentage correct vs those who submitted): 61.4%
• Average Correct Time: 31 minutes, 46 seconds.

In case Topcoder's server's are down

• You are given a rectangular grid of nodes as a vector of strings.
• The characters of the strings are digits, upper-case and lower-case values.
• The value of a digit is the digit's value.
• The values of 'a' through 'z' are 10 through 35.
• The values of 'A' through 'Z' are 36 through 61.
• You are playing a game where you are going to "activate" nodes.
• The node in cell (0,0) starts activated. The rest are not activated.
• You will proceed in turns until every node is activated.
• In each turn, you activate a non-activated node which is either horizontally or vertically adjacent to an activated node. When you activate a node, you "score" the difference between the non-activated node and the activated node to which it is connected.
• Return the maximum score of activating all nodes.
• The Topcoder constraints are vectors of size 50 with at most 50 characters. You can bump this up quite a bit, since the algorithm is O(E log V), and E = O(V), so ./gen_input uses 500 as the constraint instead of 50.

UNIX> g++ -o gen_input gen_input.cpp

Examples

# Input                    Answer

0 "05"                     69
  "aB"  

1 "03"                     7
  "21"

2 "John"                   118
  "Brus"
  "Gogo"

3 "AAA"                    0
  "AAA"
  "AAA"

Hints

First, here's a table of the values of letters, so you can process the examples easier:

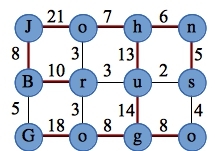
Because pictures help, here's the graph for Example 2, with its maximum spanning tree.

21+7+6+8+13+5+10+14+18+8+8 = 118. It's good practice to solve this problem with both Prim and Kruskal's algorithm.