 |
# init Answer Comments 0 125000000 1 125000000 * 8 + 7 = 1000000007. 1 281250001 2 281250001 -> 1125000007 -> 9000000063, which is 1000000007*9. 2 18426114 58 3 4530664 478 4 705616876 100000 5 852808441 -1 6 1000000006
When the rabbit is at position x, he/she can jump to two positions: (4x+3)%BP and (8x+7)%BP. You can view each position as a node on a graph, and each jump to a new position as an edge. The problem then becomes to find the shortest path to node 0. The graph is unweighted, so your job is to solve an unweighted shortest path problem using breadth-first search.
There is a little subtlety, which is common to some shortest path problems -- the graph is potentially huge! There are BP potential nodes on this graph, so we certainly cannot build it and hold it in memory. However, we don't have to hold the entire graph in memory. Instead, we build it incrementally while we do the shortest path calculation. Recall how unweighted shortest path works:
There's nothing in this algorithm that says you have to build the graph before-hand. Instead, you can create the adjacency list when you visit a node, and create the new nodes at that point if you need to.
Let's build a solution. We want each node to have two values: its id and its distance, which is the minimum number of hops from init to the node. We could define a class for nodes, and a queue of nodes for the breadth-first search. However, to make my programming easier, I'm simply going to maintain two queues of integers. The first queue holds node id's and the second holds distances. I'm going to declare them as deque's since that data structure allows you do append to the end and delete the beginning in constant time.
We start by pushing init onto our breadth-first search queue. This really means two push_back() operations -- pushing init onto our id queue and zero onto our distance queue. We'll exemplify with example #1 from the topcoder problem, where the rabbit starts at 281,250,001. In the pictures below, I'll draw the graph so far, and the queue's id and distance:
 |
Now, we process the queue as in the bulleted list above. We remove the first element from ids and distances. We test whether the id is zero. If it is, we're done. It's not, so we calculate its two edges:
For each of those edges, we push them on the queue with a distance of one:
 |
I want to stress, our program does not store the graph. That's only drawn to help you visualize the solution. We only hold the two deques. We next process id 125,000,000 with a distance of one. Here are its edges:
That looks promising. Let's push these new nodes onto ids and distances.
 |
Next we work on 250,000,001, whose distance is one. Here's the new graph:
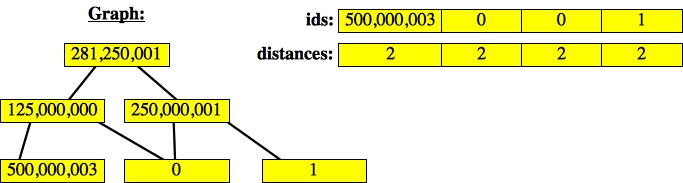 |
You'll note that node zero is on the queue ids twice. We'll deal with that later. However, it should give you a clue about how this problem does not blow up exponentially. If y = 4x+3 and z = 8x+7, then:
Whatever, we'll deal with that later. Let's process the next node on the queue -- 500,000,003:
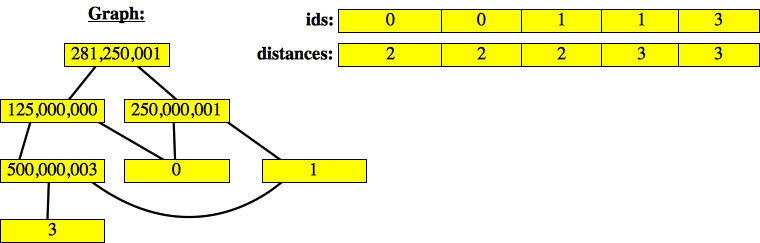 |
When we process the next node, it's id is zero, so we're done. We return the distance of two.
int CarrotJumping::theJump(int init)
{
deque <int> ids;
deque <int> distances;
int node;
int distance;
ids.push_back(init);
distances.push_back(0);
while (1) {
node = ids[0];
distance = distances[0];
ids.pop_front();
distances.pop_front();
cout << "Processing node " << node << " with a distance of " << distance << endl;
if (node == 0) return distance;
ids.push_back((node*4+3)%1000000007);
distances.push_back(distance+1);
ids.push_back((node*8+7)%1000000007);
distances.push_back(distance+1);
}
}
|
That's a nice and simple BFS. Let's run it on the first two examples (my driver program is in Carrot-Main.cpp, which includes CarrotJumping.cpp and compiles in the topcoder examples:
UNIX> cp Carrot-Jumping-1.cpp CarrotJumping.cpp UNIX> g++ Carrot-Main.cpp UNIX> a.out 0 Processing node 125000000 with a distance of 0 Processing node 500000003 with a distance of 1 Processing node 0 with a distance of 1 1 UNIX> a.out 1 Processing node 281250001 with a distance of 0 Processing node 125000000 with a distance of 1 Processing node -44967267 with a distance of 1 Processing node 500000003 with a distance of 2 Processing node 0 with a distance of 2 2 UNIX>Well, it gets the correct answer with both examples, but the node "-44967367" suggests that using integers will not work. Think about it: BP is roughly 230. So 8*BP will be roughly 233, and that's too big for an integer. Our first step is to use long long's instead of integers. That's in Carrot-Jumping-2.cpp, which I don't show here, as its just a few edits. It works on the first two examples, but chokes on example 2:
UNIX> cp Carrot-Jumping-2.cpp CarrotJumping.cpp UNIX> g++ Carrot-Main.cpp UNIX> a.out 0 Processing node 125000000 with a distance of 0 Processing node 500000003 with a distance of 1 Processing node 0 with a distance of 1 1 UNIX> a.out 1 Processing node 281250001 with a distance of 0 Processing node 125000000 with a distance of 1 Processing node 250000001 with a distance of 1 Processing node 500000003 with a distance of 2 Processing node 0 with a distance of 2 2 UNIX> a.out 2 Processing node 18426114 with a distance of 0 Processing node 73704459 with a distance of 1 Processing node 147408919 with a distance of 1 Processing node 294817839 with a distance of 2 Processing node 589635679 with a distance of 2 Processing node 589635679 with a distance of 2 Processing node 179271352 with a distance of 2 Processing node 179271352 with a distance of 3 Processing node 358542705 with a distance of 3 Processing node 358542705 with a distance of 3 .... You CNTL-C out of this and try: UNIX> a.out 2 | tail -n 1 .... And this takes forever.The problem is all of those duplicate nodes on the deques. You can solve that problem by maintaining a set of node id's, and you only push a node onto the deques when it is not in the set. That code is in Carrot-Jumping-3.cpp:
int CarrotJumping::theJump(int init)
{
deque <long long> ids;
deque <int> distances;
set <long long> nodes;
long long node, newnode;
int distance;
ids.push_back(init);
distances.push_back(0);
while (1) {
node = ids[0];
distance = distances[0];
ids.pop_front();
distances.pop_front();
if (node == 0) return distance;
newnode = (node*4+3)%1000000007;
if (nodes.find(newnode) == nodes.end()) {
ids.push_back(newnode);
distances.push_back(distance+1);
nodes.insert(newnode);
}
newnode = (node*8+7)%1000000007;
if (nodes.find(newnode) == nodes.end()) {
ids.push_back(newnode);
distances.push_back(distance+1);
nodes.insert(newnode);
}
}
}
|
That works for examples 2 through 4, and since example 4 takes a little time, we check it to see that it runs within 2 seconds -- we're good:
UNIX> cp Carrot-Jumping-3.cpp CarrotJumping.cpp UNIX> g++ Carrot-Main.cpp UNIX> a.out 2 58 UNIX> a.out 3 478 UNIX> a.out 4 100000 UNIX> time a.out 4 100000 0.930u 0.020s 0:00.95 100.0% 0+0k 0+0io 0pf+0w UNIX>We now need to handle what happens when our rabbit jumps 100001 times. He quits, and we return -1. That's an easy check of distance, which is in Carrot-Jumping-4.cpp. I've put a comment into the only new line:
...
if (distance == 100001) return -1; /* This is the only new line */
...
|
It succeeds on example 5:
UNIX> cp Carrot-Jumping-4.cpp CarrotJumping.cpp UNIX> g++ Carrot-Main.cpp UNIX> a.out 5 -1 UNIX>Time to submit? Well now is a good time to think about conditions which may trip you up. Can you think of any? I can tell you that these few lines should be a little bit of a red flag:
...
while (1) {
node = ids[0];
distance = distances[0];
...
|
Think to yourself: "Can that loop really be infinte?" and "Could the size of ids or distances be zero?" I think that the answer to the first one is "no" -- example 5 shows the longest time it will take. How about the second question. Could we run out of nodes? Maybe. Maybe our graph has nothing but cycles. If that's the case, our rabbit is going to be jumping around infinitely, and more importantly, ids and distances will become empty. So, let's fix it by testing ids, and if it's empty, we return -1.
The final code is in Carrot-Jumping-5.cpp. As it turns out, I've put case 6 into Carrot-Main.cpp, which sets init to 1,000,000,006, where (4x+3)%BP equals x. We need that test for the program to work in this case. (When I first did this problem, that case is the one that tripped me up....).
The final program is below:
#include <string>
#include <deque>
#include <set>
#include <iostream>
#include <cstdio>
#include <cstdlib>
using namespace std;
class CarrotJumping {
public:
int theJump(int init);
};
int CarrotJumping::theJump(int init)
{
deque <long long> ids;
deque <int> distances;
set <long long> nodes;
long long node, newnode;
int distance;
ids.push_back(init);
distances.push_back(0);
while (1) {
if (ids.size() == 0) return -1;
node = ids[0];
distance = distances[0];
ids.pop_front();
distances.pop_front();
if (distance == 100001) return -1;
if (node == 0) return distance;
newnode = (node*4+3)%1000000007;
if (nodes.find(newnode) == nodes.end()) {
ids.push_back(newnode);
distances.push_back(distance+1);
nodes.insert(newnode);
}
newnode = (node*8+7)%1000000007;
if (nodes.find(newnode) == nodes.end()) {
ids.push_back(newnode);
distances.push_back(distance+1);
nodes.insert(newnode);
}
}
}
|