 |
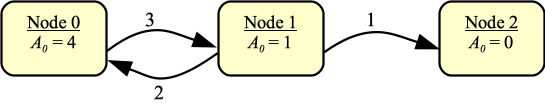
This is a wonderful Dijkstra-esque problem (and no, I didn't get it on my own).
Let's define two quantities of nodes:
 |
Next, I'm going to calculate B1 for each of the nodes. This is the shortest path that Alice can take if Bob gets to choose the edge out of each of these nodes. Since nodes 0 and 2 have at most one edge coming out of them, for them, B1 equals A0. However, with Node 1, Bob has a choice. If he chooses the edge to node 2, then the path length is one. However, if he chooses the edge to node 0, then the path length is (2 + A0(0)) = 6. Obviously, Bob will choose that edge. Here are the B1 values:
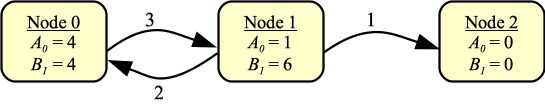 |
Time to work on A1. To restate, A1(n) is Alice's shortest path from n the last node, given that Bob has one token, meaning Bob can choose her edge exactly once:
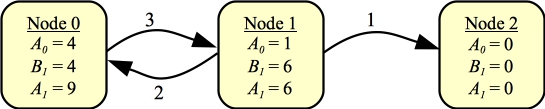 |
Once we have A1, we can calculate B2 from them. Recall that B2(n) is Alice's shortest path from node n given that Bob has two tokens, and he uses one of them on node n. The way that you determine B2(n) is to look at every edge going from n. Suppose that edge is e = (n,m). Then Bob wants to choose the edge such that (Weight(e) + A1(m)) is maximized.
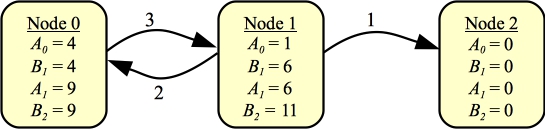 |
And let's do one more -- calculating A2. We do this from node 2 back to node 0:
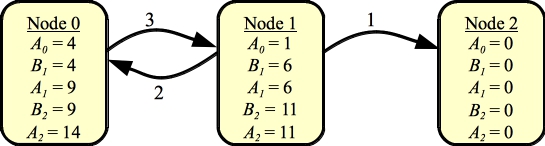 |
You can spot the pattern here -- Ai(0) equals 4+5i. This is why the answer to example zero is 5004.
I know I've walked through this very slowly, but I want you to understand how you calculate Bi from Ai-1, and how you calculate Ai from a combination of Bi and other nodes' Ai.
The heart of Dijkstra's algorithm looks as follows:
- Pull node n with distance d off of the multimap.
- For every edge from n to m, do the following:
- If we've visited m already, skip it.
- Take a look at the path length to m through n. Call this value newd.
- If newd < m's current distance, then:
- Update m's current distance to newd.
- Put m on the multimap, keyed by newd.
- (Decide what to do if m was already on the multimap. I leave it there).
|
We need to modify the heart of this algorithm to do the calculation above. Here's the psuedocode:
- Pull node n with distance d off of the multimap.
- For every edge from n to m, do the following:
- If we've visited m already, skip it.
- Take a look at the path length to m through n. Call this value newd.
- If newd < Bi(m), then set newd to Bi(m).
- If newd < m's current distance, then:
- Update m's current distance to newd.
- Put m on the multimap, keyed by newd.
- (Decide what to do if m was already on the multimap. I leave it there).
|
The line in blue is the new line. It says, "If Alice finds a path that is less than Bi(n), then Bob is going to use his token, because he doesn't want to allow Alice to use that path."
I hope this helps you understand the calculation of Ai(n). I can tell you that I had a hard time with it, which is why this writeup is so long. Have fun!
class MaliciousPath {
public:
long long minPath(int N,
int K,
vector <int> from,
vector <int> to,
vector <int> cost);
vector < vector <int> > Adj; // Adjacency lists
vector < vector <int> > Radj; // Reverse adjacency lists
vector < vector <long long> > Weights; // Weights
vector < vector <long long> > RWeights; // Reverse weights
vector <int> Visited; // Visited field for Dijkstra.
vector <long long> A; // A - I replace this for each different i.
vector <long long> B; // B - I replace this for each different i.
void FirstDijkstra(); // The Dijkstra to determine A_0
void NextDijkstra(); // The Dijkstra to determine the other A_i
long long bll; // Infinity (0x100000000000LL).
};
|
I didn't realize until after I wrote this writeup that you don't need FirstDijkstra(). You can simply set B0(n) -1, and NextDijkstra() will work for A0(n).