SRM 699, D1, 500-Pointer (FromToDivisible)
James S. Plank
Mon Dec 3 15:05:06 EST 2018
If Topcoder's Servers are Down
Here is a summary of the problem:
- You are given a graph with N nodes, numbered 1 through N.
- N may be as big as 1,000,000,000.
- You are given two vectors, a and b, which have exactly M elements.
- M may be as big as 1,000.
- Each element of a and b is a number between 1 and N.
- In the graph, there is a directed edge from node i to node j
if there exists a number k between 0 and M-1 such that
i is divisible by a[k] and
j is divisible by b[k].
- Each edge has a distance of one.
- You are given a starting node S and an ending node T.
- Compute and return the shortest path from S to T.
- If there is no path from S to T, return -1.
Examples:
| # |
N |
S |
T |
a |
b |
Answer |
| 0 |
11 |
9 |
6 |
{3,10} |
{5,2} |
2 |
| 1 |
123456789 |
18 |
12 |
{1,42,50} |
{1,17,3} |
1 |
| 2 |
60 |
30 |
8 |
{16,15,12} |
{2,20,5} |
-1 |
| 3 |
77 |
10 |
62 |
{2,5,7,4,17,26} |
{25,7,11,13,31,34} |
4 |
| 4 |
100 |
90 |
40 |
{20,30,100,99,100} |
{10,30,100,100,99} |
2 |
| 5 |
1000000000 |
7000 |
424212345 |
{35000000,120000000,424212345,200000000,3500,19} |
{15,1,7000,200000000,400000000,17} |
3 |
| 6 |
2 |
1 |
2 |
{2} |
{1} |
-1 |
| 7 |
|
|
|
See main.cpp for values. |
|
35 |
| 9 |
|
|
|
See main.cpp for values. |
|
72 |
| 14 |
|
|
|
See main.cpp for values. |
|
7 |
| 17 |
|
|
|
See main.cpp for values. |
|
140 |
| 19 |
|
|
|
See main.cpp for values. |
|
-1 |
| 22 |
|
|
|
See main.cpp for values. |
|
1 |
Grading
There are tests.sh and answers.txt files. The examples above are the only
ones in tests.sh, and they are hard-coded in
main.cpp, so I don't read anything from standard input, and there are
just 13 test problems. So be it. I could write some harder ones, but I'm not in the mood.
Your code needs to run in under 2 seconds for each example.
Intuition -- What on earth are the graphs?
You can try to draw them, but they are a pain to draw. It's probably easier
to just describe them. Try this for example 0:
- Each of nodes { 3, 6, 9 } has an edge to each of { 5, 10 }.
- Node 10 has an edge to each of { 2, 4, 6, 8, 10 }.
Given that definition, it's pretty easy to see that the shortest path from 9
to 6 goes from 9 to 10 to 6.
Hopefully that gives you some better intuition about what these graphs
look like.
Strategy -- Build a Smaller Graph with Equivalent Properties
This sure feels like an unweighted shortest path (BFS) problem. However, like
many Topcoder graph problems, you can't use the graph that they specify, but
instead, you have to create an alternate graph with equivalent properties.
Obviously, the graph that they specify is too big. If a[i] equals 2, and
b[i] equals 3, and N equals 1,000,000,000, then there are roughly
(500,000,000 * 333,333,333) edges. That's too big.
However, let's work on building a different graph that solves the problem, but is much smaller.
Here's thought number one: If your path uses an edge (w,x)
defined by (a[i],b[i]), then it will never
take a subsequent edge (y,z) which is also defined by (a[i],b[i]). Why?
Because the edge (w,z) will exist, and your path could have taken it instead of (w,x).
That observation helps us, because we can try to define our path as a sequence
of (a[i],b[i]) values, rather than as a sequence of edges of the original
graph.
So, let's build a new graph. In this new graph, the nodes are i values (as in
(a[i],b[i])). We'll have an edge from S to a node i if
the (a[i],b[i]) includes node S as one of its a[i] nodes.
And, we'll have an edge from a node i to T
the (a[i],b[i]) includes node T as one of its b[i] nodes.
Finally, we'll have an edge from node i to node j if there exists a
node that is one of the b[i] nodes, and also one of the a[j] nodes.
The shortest path from S to T on this new graph defines a shortest path on
the original graph. The path on the original graph will be one edge shorter than the
path our our new graph (we'll see this on the example below).
We can find this shortest path using BFS, which is O(|V|+|E|). Our
new graph has a maximum of 1000 nodes, so the maximum number of edges is 1,000,000. That's
big, but well within topcoder limits.
Converting the problem's graph to our alternate graph
First, how do we create the edges from S? Those will be to nodes i
such that S is a multiple of a[i]. Similarly, the nodes to T
will be the nodes i
such that T is a multiple of b[i].
What about edges from node i to node j? We need to find a node C such
that C is a multiple of b[i] and also a multiple of a[j]. In other
words, we need to find the least common multiple (LCM) of b[i] and a[j]. If that
value is less than or equal to N, then the edge exists. If it is greater to N,
then the edge doesn't exist.
Is there a fast algorithm for LCM of x and y? Yes, and it is based on finding the
greatest common denominator (GCD) of
x and y. Suppose the GCD of x and y is z. Define s
and t such that x = sz and y = tz. Then, the LCM of x and y
is zst.
There is a fast algorithm (log time) for GCD. It is attributed to Euclid, and it goes as
follows:
- Assume x is greater than y.
- Let a equal x % y.
- If a equals zero, then the GCD is y.
- Othewise, the GCD is equal to the GCD of y and a.
This gives you a way of creating the graph.
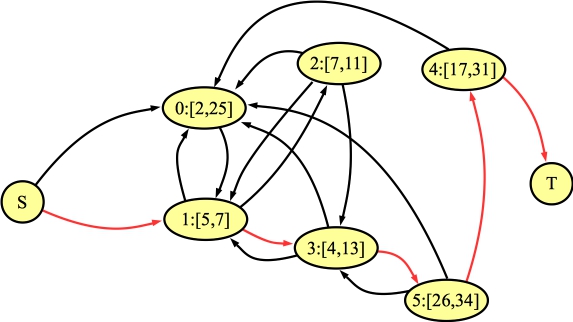
Example 3
Example 3 is big enough to be interesting.
- S is 10, which is a multiple of 2, and 5. So, there are edges from S to
nodes 0 and 1.
- T is 62, which is a multiple of 31. So, there is an edge from node 4 to T.
- Let's look at edges from node 0. b[0] is 25, so the only node whose a[i]
value has an LCM with 25 that is less than 77 is node 1. So there is an edge from node 0
to node 1.
- Let's look at edges from node 1. b[1] is 7, so it will have edges to
nodes 0, 2 and 3.
- Let's look at edges from node 2. b[2] is 11, so it will have edges to
nodes 0, 1 and 3.
- Let's look at edges from node 3. b[3] is 13, so it will have edges to
nodes 0, 1 and 5 (the LCM of 13 and 7 is 91, which is too big).
- Let's look at edges from node 4. b[4] is 31, so it will have an edge to node 0
(and of course to T).
- And let's look at edges from node 5. b[5] is 34, so it will have edges to nodes
0, 3 and 4.
That gives us the following graph:
You can see the shortest path in red - since it is composed of five edges, the answer
is four.
Now that you know all of the pieces of the
puzzle, go ahead and solve the problem!