Leetcode.com problem 2477: Minimum Fuel Cost to Report to the Capital
James S. Plank
Wed Apr 12 00:07:04 EDT 2023
In case Leetcode's servers are down
- You are given the edges of a tree.
- The edges may be in any order (in other words, the edge 0-1 is equivalent to the edge 1-0).
- The nodes are numbered from 0 to N-1.
- Each node represents a city, and each city starts with one "representative" (a person)
- Each city also starts with a car that has seats seats.
- It takes a liter of fuel for a car to travel along an edge from one node to another.
- At each city, representatives may change cars.
- What is the minimum amount of fuel necessary to get all representatives from their original
cities to city 0?
- The number of roads is between 0 and 100,000.
You are to solve this with the method minimumFuelCost of the class Solution:
class Solution {
public:
long long minimumFuelCost(vector <vector <int> > &roads, int seats);
};
|
Examples
- Example 1:
roads = [ [0,1], [0,2], [0,3] ]
seats = 5
Here's ASCII-Art of the tree:
It should be clear that representatives 1, 2 and 3 take one liter of fuel each to get to
city 0. The answer is 3.
- Example 2:
roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]]
seats = 2
Here's ASCII-Art of the tree:
3
/ \
1 2
|
0
/ \
4 5
|
6
|
This one takes some more work to figure out:
- Representative 6 goes to city 4, and then carpools with 4 to city 0: 2 liters
- Representative 5 goes to city 0: 1 liter
- Representative 2 goes to city 3, and then carpools with 3 to city 1: 2 liters
- From city 1, representatives 1, 2, and 3 need two cars to get to city 0: 2 more liters.
The total is 7 liters.
There are other examples in the examples directory.
The driver program
The program in Skeleton.cpp and
Solution.cpp reads all of the edges, plus the number of seats, from standard input.
Here are the first two examples:
UNIX> g++ Solution.cpp
UNIX> echo 0 1 0 2 0 3 5 | ./a.out
3
UNIX> echo 3 1 3 2 1 0 0 4 0 5 4 6 2 | ./a.out
7
UNIX>
Hints
The first order of business is to turn these into trees that are useful for processing.
Since our goal is for everyone to get to node zero, it makes sense for node zero to
be the root of the tree. Let's redraw examples 1 and 2 so that node zero is the
root -- I'll make these drawings nicer than ASCII art:
| Example 1: 
|
Example 2: 
|
How does this help us? Well, let's keep the following pieces of information with
each node:
- n: The number of representatives that end up at this node.
- f: The amount of fuel required to get the representatives to this node.
Here are the two example trees with this information (each node stores [n,f]).
| Example 1: 
|
Example 2: 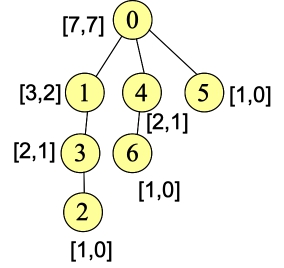
|
The answer is the value of f for node 0.
You can calculate these values of n and f by doing a postorder traversal
from node 0. For each node, you visit the node's children. Then you use the n
and f values of each of the children, combined with the number of seats
in the cars, to calculate the node's values of n and f.
I won't go through it more than that. I will give two extra hints though:
Extra Hint 1
You may wonder how to represent the tree. What I did was create a vector of children
for each node. This vector includes all of a node's children, plus its parent. So,
for the first example:
Node 0: Children 1, 2, 3.
Node 1: Children 0
Node 2: Children 0
Node 3: Children 0
|
And for the second example:
Node 0: Children 1, 4, 5.
Node 1: Children 0, 3
Node 2: Children 3
Node 3: Children 1, 2
Node 4: Children 0, 6
Node 5: Children 0
Node 6: Children 4
|
When you implement the method for the postorder traversal, include the parent of the node
as a parameter. That way, the node can skip its parent when it is visiting its children.
Extra Hint 2
If you have r representatives and s seats in a car, how many cars does it
take? When I'm confronted with a problem like this, I simply use examples. Here, let's
use s=3. Then:
1, 2 or 3 representatives: 1 car.
4, 5 or 6 representatives: 2 cars.
7, 8 or 9 representatives: 3 cars.
Can you now derive a simple formula for the number of cars, given r and s?