Where’s
the FEEB?
The
Effectiveness of Instruction Set Randomization
Ana Nora Sovarel
David Evans
Nathanael
Paul
University
of
Virginia, Department of Computer Science
http://www.cs.virginia.edu/feeb
Abstract
Instruction Set Randomization (ISR) has been proposed as a promising defense against code injection attacks. It defuses all standard code injection attacks since the attacker does not know the instruction set of the target machine. A motivated attacker, however, may be able to circumvent ISR by determining the randomization key. In this paper, we investigate the possibility of a remote attacker successfully ascertaining an ISR key using an incremental attack. We introduce a strategy for attacking ISR-protected servers, develop and analyze two attack variations, and present a technique for packaging a worm with a miniature virtual machine that reduces the number of key bytes an attacker must acquire to 100. Our attacks can break enough key bytes to infect an ISR-protected server in about six minutes. Our results provide insights into properties necessary for ISR implementations to be secure.
In a code injection attack, an attacker exploits a software vulnerability (often a buffer overflow vulnerability) to inject malicious code into a running program. Since the attacker is able to run arbitrary code on the victim's machine, this is a serious attack which grants the attacker all the privileges of the compromised process.
In order for the injected code to have the intended effect, the attacker must know the instruction set of the target. Hence, a general technique for defusing code injection attacks is to obscure the instruction set from the attacker. Instruction Set Randomization (ISR) is a technique for accomplishing this by randomly altering the instructions used by a host machine, application, or execution. By changing the instruction set, ISR defuses all code injection attacks. ISR does not prevent all control flow hijacking attacks, though; for example, the return-to-libc attack [18] does not depend on knowing the instruction set. Much work has been done on the general problem of mitigating code injection attacks, and ISR is one of many proposed approaches. Previous papers have discussed the advantages and disadvantages of ISR relative to other defense strategies [3, 12, 4]. In this paper, we focus on evaluating ISR’s effectiveness in protecting a network of vulnerable servers from a motivated attacker and consider properties necessary for an ISR implementation to be secure.
Several implementations of ISR have been proposed. Kc et al.’s design emphasized the possibility of an efficient hardware implementation [12]. They considered a processor in which a special register stores the encryption key. When an instruction is loaded into the processor, it is decrypted by XORing it with the value in the key register. The processor provides a special privileged instruction for writing into the key register and a different encryption key is associated with each process. The code section of target executable is encrypted with a random key, which is stored in the executable header information so it can be loaded into the key register before executing the program. Kc et al. evaluated their design using the Bochs emulator simulating an x86 processor with a 32-bit key register.
Barrantes et al.’s design, RISE, is not constrained by the need for an efficient hardware implementation [3]. Instead of using an encryption key register, they use a key that can be as long as the program text and encrypt each byte in the code text by XORing it with the corresponding key byte. Encryption is done at load time with a generated pseudo-random key, so each process will have its own, arbitrarily long key. Their implementation used an emulator built on Valgrind [16] to decrypt instruction bytes with the corresponding key bytes when they are executed.
Existing code injection attacks assume the standard instruction set so they will fail against an ISR-protected server. This paper presents a strategy a motivated attacker who is aware of the defense may be able to use to circumvent ISR by determining the key. Our attack is inspired by Shacham et al.’s attack on memory address space randomization [17]. Like ISR, memory address space randomization attempts to defuse a class of attacks by breaking properties of the target program on which the attacker relies (in this case, the location of data structures and code fragments in memory). Shacham et al. demonstrated that the 16-bit key space used by PaX Address Space Layout Randomization [15] could be quickly compromised by a guessing attack.
Many of the necessary conditions for our attack are similar to the conditions needed for Shacham et al.s memory randomization attack. However, since the key space used in ISR defenses is too large for a brute force search, we need an attack that can break the key incrementally. Kc et al. mention the possibility that an attacker might be able to guess parts of the key independently based on the fact that some useful instructions in x86 architecture have only one or two bytes . Our attacks exploit this opportunity.
The key contributions of this paper are:
The first quantitative evaluation of the effective security provided by ISR defenses against a motivated adversary.
An identification of an avenue of attack available to a remote attacker attempting to determine the encryption key used on an ISR-protected server.
Design and implementation of a micro-virtual machine that can be used to infect an ISR-protected server using a small number of acquired key bytes.
An evaluation of the effectiveness of two types of attack on a prototype ISR implementation.
Insights into the properties necessary for an ISR implementation to be secure against remote attacks.
Next, we describe our incremental key guessing approach. Section 3 provides details on our attack and analyzes its efficiency. Section 4 describes how an attacker could use our attack to deploy a worm on a network of ISR-protected servers. Section 5 discusses the impact of our results for ISR system designers.
The most difficult task in guessing a key incrementally is to be able to notice a good partial guess. Suppose we correctly guess the first two bytes of a four byte key. We would not be able to determine whether or not the guess is correct if the random instruction in the next two bytes executes and causes the program to crash. The result would be indistinguishable from an incorrect guess of the first two bytes. Even if the next random instruction is harmless, there is a high probability that a subsequently executed instruction will cause the program to crash in a way that is indistinguishable from an incorrect guess.
Our approach to distinguish correct and incorrect partial guesses is to use control instructions. We attempt to inject a particular control instruction with all possible randomization keys. When the guess is correct the execution flow changes in a way that is remotely observable. For an incremental attack to work, the attacker must be able to reliably determine if a partial guess is correct.
For each attempt, there are four possible outcomes:
| Apparently Correct Behavior | Apparently Incorrect Behavior | |
| Correct Guess | Success | False Negative |
| Incorrect Guess | False Positive | Progress |
Ideally, a correct guess would always lead to distinguishably “correct” behavior, and an incorrect guess would always lead to distinguishably “incorrect” behavior. Given sufficient knowledge of the target system, we should be able to construct attacks where a correct guess never produces an apparently incorrect execution (barring exogenous events that would also make normal requests fail). However, it is not possible to design an attack with perfect recognition: some incorrect guesses will produce behavior that is remotely indistinguishable from that produced by a correct guess. For example, an incorrect guess may decrypt to a harmless instruction, and some subsequently executed instruction may produce the apparently correct execution behavior.
We present attacks based on two different control instructions: return, a one-byte instruction, and jump, a two-byte instruction. For both attacks, if the guess is incorrect, there is a high probability that executing random instructions will cause the process to crash. If the guess is correct, the attacker will observe different server behavior: recognizable output for the return attack and an infinite loop for the jump attack.
Next we describe conditions necessary for the attacks to succeed, explain how each attack is done, and how an incremental attack can be carried out on a large key. For both attacks, there are situations where an incorrect guess produces the same behavior as a correct guess and complications that arise in guessing larger keys. In Section 3, we discuss those issues in more detail and analyze the expected number of attempts required for each attack.
In order for the attack to be possible, the attacker must have some way of injecting code into the target system. We assume the application is vulnerable to a simple stack-smashing buffer overflow attack, although our attack does not depend on how code is injected into the randomized program. It depends only on a vulnerability that can be exploited to inject and execute code in the running process.
Our attack is only feasible for vulnerabilities where the attacker can inject code to a fixed memory location. In a normal stack-smashing attack, the attacker sometimes cannot determine the exact location where code will be inserted because of variations in system libraries, operating system patches and configurations [13]. A common solution is to pad the injected code with nop instructions, often referred to as a nop sled [2]. The attack will succeed as long as the return address is overwritten with an address that is in the range of injected nop instructions. When building an attack against an application protected by ISR, the attacker cannot use this approach because the encryption masks for the positions where nop instructions should be placed are unknown. Another technique, called a register spring [7], overwrites the return address with the address of an instruction found in the application or a library that will indirectly transfer control to the buffer, such as jmp esp or call eax. These instructions are not likely to appear normally in the code, but it is sufficient for an attacker to locate one of the instructions as operand bytes or overlapping bytes in the code segment. Sapphire used a register spring technique by jumping to a jmp esp found in sqlsort.dll [10].
The 32-bit or longer key typically used for ISR is too large for a practical brute force attack, so we must determine the key incrementally. The attacker must be able to acquire enough key bytes to inject the malicious code before the target program is re-randomized with a different key. Since our attack will necessarily crash processes on the target system, it requires either that application executions use the same randomization key each time the target application is restarted, or that the target application uses the same key for many processes it forks. A typical application that exhibits this property is a server that forks a process to serve each client’s request. Since failed guess attempts will usually cause the executing process to crash, the attacker must have an opportunity to send many requests to a server encrypted with the same key. Many servers create separate processes to handle simultaneous requests. For example, Apache (since version 2.0), provides configuration options to allow both multiple processes and multiple threads within each process to handle simultaneous requests [1].
Since our attack depends on being able to determine the correct key mask from observing correct guesses, the method used to encrypt instructions must have the property that once a ciphertext-plaintext pair is learned it is possible to determine the key. The XOR encryption technique used by RISE [3] trivially satisfies this property. Kc et al. suggest two possible randomization techniques: one uses XOR encryption and the other uses a secret 32-bit transposition [12]. The XOR cipher, which is what their prototype implements, is vulnerable to our attack. Our attack would not work without significant modification on the 32-bit transposition cipher. Learning one ciphertext-plaintext pair would reduce the keyspace considerably, but is not enough to determine the transposition. Thus, several known plaintext-ciphertext pairs would be needed to learn the transposition key.
The final requirement stems from the remote attacker’s need to observe enough server behavior to distinguish between correct and incorrect guesses. If the attack program communicates with the server using a TCP connection it can learn when the process handling the request crashes because the TCP socket is closed. If the key guess is incorrect, the server process will (usually) crash and the operating system will close the socket. Hence, the server must have a vulnerability along an execution path where normal execution keeps a socket open so the remote attacker can distinguish between the two behaviors. If the normal execution flow would close the connection with the client before returning from the vulnerable procedure, the attacker is not able to easily observe the effects of the injected code. The return attack has additional requirements, described in the next section. In cases where those requirements are not satisfied, the (slower) jump attack can be used.
The return attack uses the near return (0xc3) control instruction [11]. This is a one byte instruction, so it can be found with at most 256 guesses.
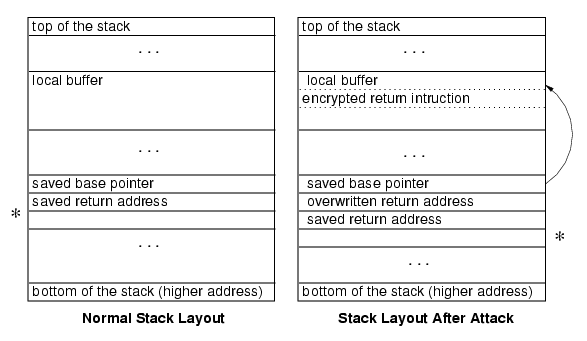
Figure 1 shows the stack layout before and after the attack. The attack string preserves the base pointer, replaces the original return address with the target address where the injected code is located, and places the original return address just below the overwritten address. When the routine returns it restores the base pointer register from the stack and jumps to the overwritten return address, which is now the injected instruction. If the guess is correct, the derandomized injected code is the return instruction. When it executes, the saved return address is popped from the stack and the execution continues as if the called routine returned normally.
There is one important problem, however. When the guess is correct, the return statement that is executed pops an extra element from the stack. In Figure 1, the star marks the position of the top of the stack in normal case (left) and after the injected code is executed successfully (right). After returning from the vulnerable routine, the stack is compromised because the top of the stack is now one element below where it should be. This means the server is likely to crash soon even after a correct guess since all the values restored from the stack will be read from the wrong location.
Thus, the return attack can only be used to exploit a
vulnerability at a location where code that sends a response to the
client will execute before the compromised stack causes the program
to crash. Otherwise, the attacker will not be able to distinguish
between correct and incorrect guesses since both result in server
crashes. An obvious problem is caused by a subsequent return.
At the next return instruction, corresponding to the return from the method
that called the vulnerable method, the actual return address is one
element up the stack from the location that will be used. It is very
likely that the element on the stack interpreted as the return address
will be an illegal memory reference. Even when the memory reference is
legal, it is unlikely to jump to a location that corresponds to the
beginning of a valid instruction.
So, the return attack can only be used effectively for vulnerabilities in which observable server activity (such as a message back to the attack client) occurs between the guessed return and the first instruction that would cause the server to crash (which at the latest, occurs at the end of the called vulnerable routine, but often occurs earlier). We suspect situations where the return attack can be used are rare, but an attacker who is fortunate enough to find such a vulnerability can use it to break an ISR key very quickly.
 |
| Figure 1. Return attack. |
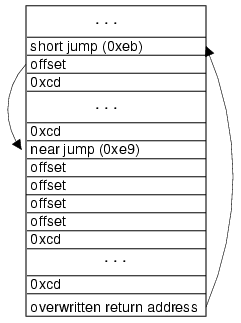
For vulnerabilities where the return attack cannot succeed, we can use the jump attack instead. The advantage of the jump attack is it can be used on any vulnerability where normal behavior keeps a socket open to the client. However, it requires guessing a two-byte instruction, instead of the one-byte return instruction. Another disadvantage of the jump attack is that it produces infinite loops on the server. This slows down server processing for further attack attempts (and may also be noticed by a system administrator). We will present techniques for substantially reducing both the number of guess attempts required and the number of infinite loops created in Section 3.2.
The jump attack is depicted in Figure 2. As with the return attack, the jump attack overwrites the return address with an address on the stack where a jump instruction encrypted with the current guess is placed. The injected instruction is a near jump (0xeb) instruction with an offset -2 (0xfe). If the guess is correct it will jump back to itself, creating an infinite loop. The attacker will see the socket open but receive no response. After a timeout has expired, the attacker assumes the server is in an infinite loop. Usually, an incorrect guess will cause the process handling the request to crash. This is detected by the attacker because the socket is closed before the timeout expires.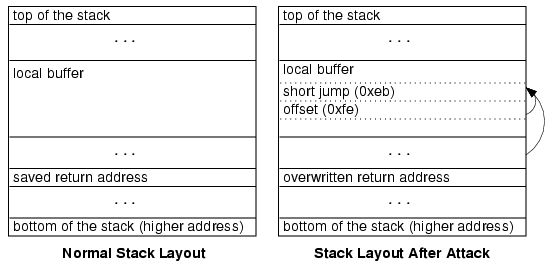 |
| Figure 2. Jump attack. |
After the first successful guess, the attacker has obtained the encryption key for one (return attack) or two (jump attack) memory locations. Since other locations are encrypted with different key bits, however, finding one or two key bytes is not enough to inject effective malicious code.
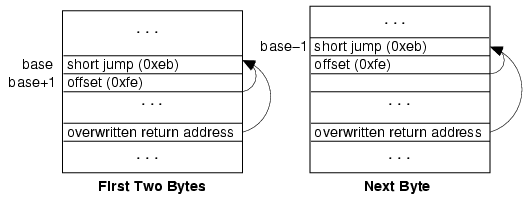
The next step is to change the position of the guessed key byte. For the return attack, we just advance to the next position and repeat the attack using the next position as the return address. With the jump attack, the attacker needs up to obtain the first two key bytes at once, but can proceed in one byte at a time thereafter. On the first attack, shown in the left side of Figure 3, the positions base and base+1 of the attack string are occupied by the jump instruction. On the second attack, we attempt to guess the key at location base–1. Since we already know the key for location base, we can encode the offset value -2 at that location, and can guess the key for the jump opcode with at most 28 attempts.
During the incremental phase of the attack, we decrement the return address placed on the stack for each memory location we guess. At some point the last byte of the address will be zero. This address cannot be injected using a buffer overflow exploit, because it will terminate the attack string before the other bytes can be injected. To deal with this case we introduce an extra jump placed in a position where we already know the encryption key and whose address does not contain a null byte. The return address will point to this jump, which will then jump to the position for which we are trying to guess the key.
When a repeated 32-bit randomization key is used (as in [12]), the number of attempts required to acquire the key using the straightforward attacks would be at most 1024 (4´28) for the return attack and 66,048 (216+2´28) for the jump attack (extra attempts may be needed to distinguish between correct guesses and false positives, as explained in the next section). For ISR implementations, such as RISE [3], that do not use short repeated keys the attacker may need to obtain many key bytes before the malicious code can be injected. This cannot be done realistically with the approach described here. Section 3 describes techniques that can be used to make incremental key breaking more efficient. Section 4 explains how many key bytes an attacker will need to compromise to inject and propagate an effective worm.
 |
| Figure 3. Incremental jump attack. |
The main difficulty in getting the attack to work in practice is that an incorrect guess may have the same behavior as the correct guess. In order to determine the key correctly, the attacker needs to be able to identify the correct key byte from multiple guesses with the same apparently correct server behavior. The next two subsections explain how false positives can be eliminated with the return and jump attacks respectively. Section 3.3 describes an extended attack that can be used to break large keys.
There are three possible reasons a return attack guess could produce the apparently correct behavior:
The correct key was guessed and the injected instruction decrypted to 0xc3.
An incorrect key was guessed, but the injected instruction decrypted to some other instruction that produced the same observable behavior as a near return.
The injected instruction decrypted to an instruction that did not cause the process to crash, and some subsequently executed instruction behaved like a near return.
The first case will happen once in 256 guess attempts.
There are several guesses that could produce the second outcome. The most likely is when the injected instruction decrypts to the 3-byte near return and pop instruction, 0xc2 imm16. The near return and pop has the same behavior as the near return instruction, except it will also pop the value of its operand bytes off the stack. Hence, if the current stack height is less than the decrypted value of the the next two bytes on the stack, the observed behavior after a 0xc2 instruction may be indistinguishable from the intended 0xc3 instruction. In the worst case, the stack is high enough for all values to be valid and we will have a false positive corresponding to 0xc2 once every 256 guess attempts.
There are two other types of instructions that can also produce the apparently correct behavior: calls and jumps. In order to produce the near return behavior, the 4-byte offset of the call or jump instruction must jump to the return address. The probability of encountering such a false positive is extremely remote (approximately 2-36). Thus, we ignore this case in our analysis and implementation; this has not caused problems in our experiments.
Given that we observe the return behavior, we can estimate the probability that the correct mask was guessed. We use ph to represent the probability an arbitrarily long random sequence of bits will start with a harmless instruction. We consider any instruction that does not cause the execution to crash immediately after executing it to be harmless (even though it may alter the machine state in ways that cause subsequent instruction to produce a crash). Instruction lengths vary, so determining whether a given injected byte is harmless may depend on the subsequent bytes on the stack. The value of ph depends on the current state of the execution. Whether or not a given instruction produces a crash depends on the execution’s address space, as well as the current values in registers and memory.
We use pr to represent the probability a random sequence of bits on the stack exhibits the same behavior as the near return instruction, thus capturing cases 1 and 2 above. As we have defined it, the harmless instructions include instructions that behave like the near return. We use phnr = ph – pr to denote the probability random bits correspond to a harmless instruction that does not behave like a near return. Then, we can estimate the probability that a guess produces the apparently correct behavior as:
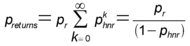 |
Given that we observe the correct behavior for some guess, the conditional probability that the guess was actually correct is:
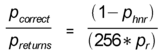 |
The actual values of ph and pr depend on the execution state. For our test server application (described in Section 5.1), we compute pr as 1/256 (probability of guessing 0xc3) + 1/256 (probability of guessing 0xc2) ´ 10588/216 (fraction of immediate values that do not cause a crash) = 0.00454. In our experiments (described in Section 5.3), we observed the apparently correct behavior with probability 0.0073. The false positive probability is 0.0034. From this, we estimate ph = 0.43. Thus, 57% of the time an execution will crash on the first random instruction inserted.
Eliminating False Positives
For each memory location for which we want to learn the randomization key, a straightforward implementation guesses all 255 possibilities. We cannot guess the mask 0xc3 using a string buffer overflow attack, since this would require inserting a null byte. If none of the 255 attempts produce the return behavior, we conclude that the actual mask is 0xc3.
If
more than one guess produces the apparently correct behavior, we place
a known harmless instruction at the guessed position followed by a
previously injected guess that produced the return behavior at the next
stack position as shown in Figure 4. If this attempt does not exhibit
the apparently correct behavior, we can safely eliminate the guessed
mask since we know the injected byte did not decrypt to a harmless
one-byte instruction as expected. Note that we do not need to know the
exact mask for the next position, just a guess we have previously
learned produces the return behavior at that location. This approach
allows us to distinguish correct guesses from false positives at all
locations except for the bottom address (the first one we guess since
we are guessing in reverse order on the stack). In cases where multiple
guesses are possible for the bottom location, we use its guessed mask
only to eliminate false positives in the other guesses, but do not use
that location to inject code.
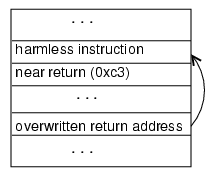
Figure 4. Eliminating false positives.
Harmless instructions help us eliminate false positives for two reasons. If the guess is correct they have known behavior; otherwise, they may decrypt to either a harmful instruction or to an instruction with a different size that will alter the subsequent instructions. In the second case, it is possible to still produce the apparently correct behavior when the mask guess is incorrect. Hence, we learn conclusively when a mask is incorrect, but still cannot be sure the guess is correct just because it exhibits the correct behavior.
The number of useful harmless one-byte instructions is limited by the density of x86 instruction set. If there are groups of harmless instructions with similar opcodes, it is hard to differentiate between them. Harmless instructions are only useful if an incorrect mask guess encrypts the guessed harmless instruction to an instruction that causes a crash. For example, if we use as harmless instructions a group of similar instructions such as clear carry flag (0xf8), clear direction (0xfc), complement carry flag (0xf5), set carry flag (0xf9), set direction flag (0xfd), the number of masks eliminated is in most of the cases is the same as if we had use only one of these instructions. Our attack uses three disparate one-byte harmless instructions: nop (0x90), clear direction (0xfc), and increment ecx register (0x42).
For a given set of possible masks it would be possible to determine a minimal set of distinguishing harmless instructions, however this would add substantially to the length and complexity of the attack code. Instead, in the rare situations where the three selected one-byte harmless instructions are unable to eliminate all but one of the guessed masks, we use harmless two-byte instructions, of which there are many. This approach works for all locations except the next-to-bottom address. In the rare situations when it is not possible to determine the correct mask for this location, we can simply start the injected attack code further up the stack.
Using harmless one-byte and two-byte instructions we are able to reduce the number of apparently correct masks to at most two. We cannot handle the case where the first instruction decrypts to a near return and pop instruction (0xc2 imm16) using this elimination process described because the near return (0xc3) and near return and pop (0xc2) opcodes differ by only their final bit. There is no harmless x86 instruction we can use to reliably distinguish them. When a harmless instruction is encrypted with an incorrect mask and decrypted with the correct masks, the opcode of the instruction executed differs only by one bit from the guessed harmless instruction. It is likely that this instruction will be a harmless instruction too.
To distinguish between the two forms of near return we place the bytes 0xc2 0xff 0xff on the stack using the guessed masks. This is a near return which pops 65,535 bytes from the stack. For many target vulnerabilities (including our test server), this is enough to generate a crash. To use this approach, we need to already know the next two masks on the stack. This is not a problem because we start elimination from the bottom of the stack. The first two times we apply elimination with 0xc2 we have to execute an attempt for each combination of possible masks of the next two positions. After that, we know the correct masks for the locations where we place the 0xffff.
For target applications for which popping 65,535 bytes from the stack does not cause a crash, we can use another type of elimination. After we guess enough bytes, we use a jump instruction to eliminate incorrect masks. We place a jump instruction with its offset encrypted using one of the apparently correct guessed masks. The jump instruction when the mask is correct will cause a jump to a memory location where a near return is placed.
Once we have determined six or more masks, we can take advantage of additional injected instructions to further minimize the likelihood of false positives and improve guessing efficiency. These techniques are similar for both the return and jump attacks, and are described in Section 3.3.
Because it involves guessing a 2-byte key and the distinguishing behavior is less particular, the jump attack is more prone to false positives than the return attack. Fortunately, the structure of the x86 instruction set can be used to take advantage of the false positives to improve the key search efficiency.
There are four possible reasons the apparently correct behavior is observed for a jump attack guess:
The correct key was guessed and the injected instruction decrypted to a jump with offset -2.
The injected guess decrypted to some other instruction which produces an infinite loop.
The injected instruction decrypted to a harmless instruction, and some subsequently executed instruction produces an infinite loop.
The injected guess caused the server to crash, but because of network lag or server load, it still took longer than the timeout threshold the attacker uses to identify infinite loops.
We can avoid case 4 by setting the timeout threshold high enough, but this presents a tradeoff between attack speed and likelihood of a false positive. A more sophisticated attack would dynamically adjust the timeout threshold. Since case 4 is likely to occur for many guesses and will not occur repeatedly for the same guess, case 4 is usually distinguishable from the other three cases and the attacker can increase the timeout threshold as necessary.
From a single guess, there is no way to distinguish between case 1 (a correct guess) and cases 2 and 3. However, by using the results from multiple guesses, it is possible to distinguish the correct guesses in nearly all instances.
For the second case, there are two kinds of false positives to consider: (1) the opcode decrypted correctly to 0xeb, but the offset decrypted to some value other than -2 which produced an infinite loop; or (2) the opcode decrypted to some other control flow instruction that produces an infinite loop.
An example of the first kind of false positive is when the offset decrypts to -4 and the instruction at offset -4 is a harmless two-byte instruction. This is not a big problem, since, as we presented in Section 2.3, except for when we are guessing the first two bytes we are encrypting the offset with a known mask. When it does occur in the first two bytes, the attacker has several possibilities. One is to ignore this last byte and use only the memory locations above it. Another possibility is to launch different versions of the injected attack code, one for each possibly correct mask. Sometimes it would be faster to launch four versions of the attack code, one of which will succeed, than to determine a single correct mask at the bottom location.
The second case, where the opcode is incorrect, is more interesting. The prevalence of these false positives, and the structure of the x86 instruction set, can be used to reduce the number of guesses needed. The other two-byte instructions that could produce infinite loops are the near conditional jumps. Like the unconditional jump instruction, the first byte specifies the opcode and the second one the relative offset. There are sixteen conditional jump instructions with opcodes between 0x70 and 0x7f. For example, opcode 0x7a is the JP (jump if parity) instruction, and 0x7b is the JNP (jump if not parity) instruction. Regardless of the state of the process, exactly one of those two instructions is guaranteed to jump. Conveniently, all the opcodes between 0x70 and 0x7f satisfy this complementary property. Thus, for any machine state, exactly 8 of the instructions with opcodes between 0x70 and 0x7f will jump, producing the infinite loop behavior if the mask for the offset operand is correctly guessed. When we find several masks sharing the same high four bits of the first byte that all produce infinite loops, we can be almost certain that those four bits correspond to 0x7.
We can take further advantage of the instruction set structure by observing that if we try both guesses for the least significant bit in the opcode, we are guaranteed that one of the two guesses will produce the infinite loop behavior if the first four bits of the guess opcode are 0x7. That is, if we guess two complementary conditional jump instructions, one of them will produce the infinite loop behavior; it doesn’t matter what the other three bits are, since all of the conditional jump opcodes have the same property.
This observation can be used to substantially reduce the number of attempts needed. Instead of needing up to 256 guesses to try all possible masks for the opcode byte, we only need 32 guesses (0x00, 0x10, 0x20, ..., 0xf0, 0x01, 0x11,...,0xf1) to try both possibilities for the least significant bit with all possible masks for the first four bits. Those 32 guesses always find one of the taken conditional jump instructions. Hence, the maximum number of attempts needed to find the first infinite loop (starting with no known masks) is 213 (25 guesses for the opcode ´ 28 guesses for the offset). When the offset is encrypted with a known mask (that is, after the first two byte masks have been determined), at most 32 attempts are needed to find the first infinite loop. The expected number of guesses to find the first infinite loop is approximately 15.75 since we can find it by either guessing a taken conditional jump instruction or the unconditional jump. (This analytical result is approximate since it depends on the assumption that each conditional jump is taken half the time. Since the actual probability of each conditional jump being taken depends on the execution state, the actual value here will vary slightly.)
After finding the first infinite loop producing guess, we need additional attempts to determine the correct mask. The most likely case (15/16ths of the time), is that we guessed a taken conditional jump instruction. If this is the case, we know the first four bits unmask to 0x7, but do not know the second four bits. To find the correct mask, we XOR the guess with 0x7 Å 0xe and guess all possible values of the second four bits until an infinite loop is produced. This means we have found the 0xeb opcode and know the mask. Thus, we expect to find the correct mask with 8 guesses. The other 1/16th of the time, the first loop-producing guess is the unconditional jump instruction. We expect to find two infinite loops within first four attempts. If we find them, we know we guessed the correct mask; otherwise we continue. We expect on average to use 15.75 guesses to find the first infinite loop and 7.75 guesses to determine the correct mask. Hence, after acquiring the first two key bytes, we expect to acquire each additional key byte using less than 24 guesses on average, while creating two infinite loops on the server.
In rare circumstances, the first infinite loop encountered could be caused by something other than guessing an unconditional or conditional jump instruction. One possibility is the loop instruction. The loop instruction can appear to be an infinite loop since it keeps jumping as long as the value in the ecx register is non-zero. When ecx initially contains a high value the loop instruction can loop enough times to exceed the timeout for recognizing an infinite loop. There are several possible solutions: wait long enough to distinguish between the jump and the loop, find a vulnerability in a place where ecx has a low value (an attacker may be able to control the input in such a way to guarantee this), or to use additional attempts with different instructions to distinguish between the loop and jump opcodes. For simplicity, we used the second option: in our constructed server, the ecx register has a small value before the vulnerability.
The other possibility is the injected code decrypts to a sequence of harmless instructions followed by a loop-producing instruction. This is not as much of a problem as it is with the return attack since the probability of two random bytes decrypting to a loop-producing instruction is much lower than the probability of a single random byte decrypting to a return instruction. Further, when it does occur, the structure of the conditional jumps in the instruction set makes it easy to eliminate incorrect mask guesses. The probability of encountering an infinite loop by executing random instructions was found by Barrantes, et al. to be only 0.02% [3]. However, since we are not guessing randomly but using structured guesses, the probability of creating infinite loops is somewhat higher. In the first step of the attack we generate all possible combinations for first two bytes. An infinite loop is created by an incorrect guess when first byte decrypts to a harmless one-byte instruction, and the second byte decrypts to a conditional or unconditional jump instruction, and the third byte decrypts to a small negative value. In this case both -2 and -3 will create infinite loops. To avoid false positives and increased load on the server, after we find the first infinite loop, we change the sign bit of the third byte. This changes the value to a positive one. If the loop was created by an incorrect mask, when we verify the mask with conditional jumps and fail to find the expected infinite loops we can conclude the mask guess is incorrect.
The techniques described so far are adequate for obtaining a small number of key bytes. For ISR implementations that use a short repeated key, such as [12], obtaining a few key bytes is enough to inject arbitrarily long worm code. For ISR implementations that use a long key, however, an attacker may need to acquire thousands of key byte masks before having enough space to inject the malicious code. Acquiring a large number of key bytes with the jump attack is especially problematic since attempts leave processes running infinite loops running on the server. After acquiring several key bytes this way, the server becomes so sluggish it becomes difficult to distinguish guess attempts that produce crashes from those that produce infinite loops.
Once we have learned a few masks, we can improve the attack efficiency by putting known instructions in these positions. With the jump attack, once we have guessed four bytes using short jumps, we change the guessed instruction to a near jump (0xe9). Near jump is a 5-byte instruction that takes a 4-byte offset as its operand. This is long enough to contain an offset that makes the execution jump back to the original return address. Hence, we no longer need to create infinite loops on the server to recognize a correct guess: we recognize the correct guess when the server behaves normally, instead of crashing.
When the server has the properties required
by the return attack, we will encounter false positives for the near
jump guessed caused by a relative call (0xe8). Since the opcode differers from the near
jump opcode in only one bit, we are not able to reliably distinguish
between the two instructions using harmless instructions. Instead, we
keep both possible masks under consideration until the next position
is guessed, and then identify the correct mask by trying each guess for
the offset mask. At worst, we need four times as many attempts because
it is possible that there are two positions with two possible masks in
the offset bytes. Despite requiring more attempts, this approach is
preferable to the short jump guessing since it reduces the load on the
server created by infinite loops.
 |
| Figure 5. Extended attack. |
Once we have acquired eight masks, we switch to the extended attack illustrated in Figure 5. The extended attack requires a maximum of 32 attempts per byte, and expected number of 23.5. The idea is to use a short jump instruction to guess the encryption key for current location with an offset that transfers control to a known mask location where we place a long jump instruction whose target is the original return address. The long jump instruction is a relative jump with a 32 bit offset. Hence, we need to acquire four additional mask bytes before we can use the extended attack with the jump attack.
To eliminate false positives, we inject bytes that correspond to an interrupt instruction in the subsequent already guessed positions. Interrupt is a two-byte instruction (0xcd imm8). The second byte is the interrupt vector number. When the guessed instruction decrypts to a harmless instruction, the next instruction executed will be 0xcdcd (INT 0xcd) which causes a program crash. The only value acceptable for the interrupt vector number in user mode when running on a Linux platform is 0x80 [5]. The key is to place enough 0xcd bytes in the region such that when the first instruction decrypts to some harmless non-jump instruction (which could be more than one byte), the next instruction to execute is always an illegal interrupt. Once we have room for six 0xcd bytes, we encounter no false positives.
If any of the masks in this region are 0xcd, we cannot place a 0xcd byte at that location since injecting the necessary instruction which would require injecting a null byte. In this case, we place an opcode corresponding to a two-byte instruction (we use AND, but any instruction would work). The 0xcd will be the second byte of the two-byte instruction. After the two-byte instruction it will find a 0xcd which causes a crash.
The most important advantage of this approach is that the only cases when the server sends the expected response are when (1) the first instruction executed is a taken unconditional jump; or (2) the first instruction executed is a conditional jump where the condition is true. With the return attack there is a third case: the first instruction executed is a near return. This possibility can be eliminated using the techniques described in Section 3.1.
The other advantage of this attack is that it does not need to create infinite loops on the server. Once we have enough mask bytes to inject a long jump instruction, we can distinguish correct guesses without putting the server in an infinite loop. Instead, the attacker is able to recognize a correct guess when it receives the expected response from the server.
If the malicious code is small (for example, the Sapphire worm was 376 bytes [9]), we can acquire enough key bytes to inject it directly. This is reasonable if we are attacking a single ISR-protected machine using this approach and can run our attack client code on a machine we control to obtain enough key bytes to inject the malicious code. If the attacker wants to propagate a worm on a network of ISR-protected servers, however, the worm code needs to contain all the code for implementing the incremental key attack also. This may require acquiring more key bytes than can be done without the system administrator noticing the suspicious behavior and re-randomizing the server. Since the ISR-breaking code is inherently complex, even if the malicious payload is small many thousands of key bytes would be needed to inject the worm code.
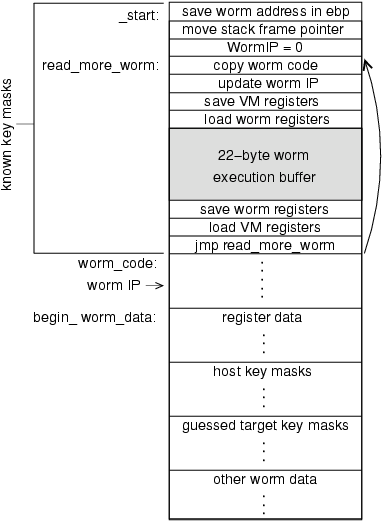
Our strategy is to instead inject a micro virtual machine (MicroVM) in the region of memory where we know the key masks. The MicroVM executes the worm code by moving small chunks of it at a time into the region where the key masks are known. The next subsections describe the MicroVM and how worm code can be written to work within our MicroVM. In order to make the MicroVM as small as possible we place restrictions and additional burdens on the worm code.
The MicroVM is illustrated in Figure 6. At the heart of the MicroVM is a loop that repeatedly reads a block of worm code into a region of memory where the masks are known and executes that code. The code (shown in Appendix A) is 98 bytes long (including the 22 bytes of space reserved for executing worm code).
 |
| Figure 6. MicroVM. |
Before starting the execution loop, the MicroVM initializes the worm instruction pointer (WormIP) to contain 0 to represent the beginning of the worm code. The WormIP stores the next location to read a block of worm code. Next, a block of worm code is fetched by copying the bytes from the worm code (from the WormIP) into an execution buffer inside the MicroVM itself, so that execution can simply continue through the worm code and then back into the MicroVM code without needing a call. The addresses of the beginning of the worm code and worm data space are hardcoded by the worm code into the MicroVM when it is deployed on a new host.
No encryption is necessary when worm code is copied into the execution buffer, since the worm code was already encrypted with known key masks for the worm execution buffer locations where it will be loaded into the worm execution buffer.
Just before the execution of the worm block, the MicroVM pushes its registers on the stack and then restores the worm’s registers from the beginning of the worm data region. After the buffer’s execution, the MicroVM saves the worm’s registers to the worm data region. In the last step, the MicroVM restores its registers and then jumps back to the beginning of the MicroVM code to execute the next block of worm code.
To work in the MicroVM, the worm code is divided into blocks matching the size of the worm execution buffer (22 bytes in our implementation). No instruction can be split across these blocks, so the worm code is padded with nops as necessary to prevent instructions from crossing block boundaries. The worm code cannot leave data on the execution stack at the end of a block, since the MicroVM registers are pushed on the stack just before the worm execution begins. To use persistent data, the worm must write into locations in the worm data space instead of using the execution stack.
The most cumbersome restrictions involve jumps. Any jump can occur within a single worm block, but jumps that transfer control to locations outside the buffer must be done differently since all worm code must executed at known mask locations in the worm buffer. Our solution is to require that all jumps must be at the end of a worm code block, and all jump targets must be to the beginning of a worm code block. Instead of actually executing a jump, the worm code updates the value of the WormIP (which is now stored in a known location in memory, and will be restored when the MicroVM resumes) to point to the target location, and then continues into the MicroVM code normally so the target block will be the next worm code block to execute. To implement a conditional jump, we use a short conditional jump with the opposite condition within the worm buffer to skip the instruction that updates the WormIP when the condition is unsatisfied.
To propagate, the worm uses the techniques described in Section 3 to acquire enough key bytes to hold the MicroVM. Those key bytes are stored in the worm data region. The MicroVM code is 98 bytes long so at least 98 key bytes are needed. We may need to acquire a few additional key bytes to avoid needing to place null bytes in the attack code. If the mask found for a given location matches the bytes we want to put there, we instead put a nop instruction at that location and obtain an extra key byte. As long as the masks are randomly distributed, two or fewer will be sufficient over 99% of the time, so we can nearly always inject the worm once 100 key bytes have been acquired.
To generate an instance of the worm for a new key, we XOR out the old key bytes from the worm code and XOR in the new key bytes. To support this, the propagated worm data includes th host’s acquired mask bytes. As with the injected MicroVM code, we need to worry about the impossibility of injecting null bytes. We insert nops in the injected worm code as necessary to avoid null bytes. If the added nops would cause a worm code block to exceed the available space, we need to create a new block and move the overflow instructions into that block. Jump targets in the worm code may need to be updated to reflect insertion of the new block.
To test our attack we built a small echo server with a buffer overflow vulnerability. The application waits for a client to connect. When the client connects, the server forks a process to process its request. The next step is to call a method which has a local buffer that can be overflowed. This method reads the request from the client and writes back an acknowledgment message. After this method call the application sends a termination message (“Bye”) and closes the socket. Although we use a contrived vulnerability to make the attack easier to execute and analyze, similar vulnerabilities are found in real applications.
The attack client structure is the same for both the jump and return attacks. For each guess attempt, the attack client (1) opens a socket to the server, (2) builds an attack string, (3) writes it to the socket, (4) reads the acknowledgment, (5) installs an alarm signal handler, (6) sets up an alarm, and (7) reads the termination message or handles the alarm signal. The return attack recognizes a possibly correct guess when it receives the termination message in step 7; the jump attack recognizes a possibly correct guess when the alarm signal handler is called before the socket is closed.
The attack strategy used for different key bytes is depicted in Figure 7. The number of key bytes guessed by the attack is denoted by size. For vulnerabilities suitable for the return attack, the first eight positions are guessed using the return instruction. The rest are guessed using the extended short jump attack (expected 23.5 attempts per byte). For the jump attack, the first two key bytes acquired have positions size-1 and size-2. We guess those two bytes simultaneously, using the 2-byte jump instruction to create an infinite loop. The next two bytes are guessed separately using the jump instruction to create an infinite loop. After the fourth byte is acquired, we do not (intentionally) create any more infinite loops. For the next six bytes, we use near jump, with a worst case of 1024 attempts per byte. After this position, we use the extended short jump attack.
 |
| Figure 7. Guessing strategies. |
For the attack client to be efficient there are some constraints on the address where the attack starts. For both attacks the address has to be far enough from the next smaller address which has null as its last byte so we have enough space to place two short jump instructions, and a sufficient number of illegal opcodes. As long as the vulnerable buffer is sufficiently large, the attack client can find a good location to begin the attack.
We ran our client normally, not inside the MicroVM. Hence, our results correspond to the time needed to launch the initial attack on the first ISR-protected server. The attack time would increase for later infections because of the additional overhead associated with executing in the MicroVM.
We executed our attack on our constructed vulnerable server protected by RISE [3]. The RISE implementation presents a major difficulty in executing our attack because of the way it implements fork, pthreads and randomization keys. This necessitated a small modification to RISE in order for our attack to succeed. Other ISR implementations, however, may be vulnerable to our attack without needing this modification.
RISE uses a different key to randomize an application each time it is started. Since the attack causes the server to crash, the attack can only work against a server that forks separate processes to handle client requests. Valgrind [16] (the emulator modified to implement RISE) implements pthreads to use only one process. Thus, if the attack crashes a thread, then the entire server will crash and the next execution will use a different randomization key. So, our attack will only work against a server that forks separate processes.
When RISE loads an application, a cache data structure is initialized that holds the key mask for each instruction address that has been loaded. There is a different randomization key byte for each byte in the text segment, and the mask value is stored in the cache the first time the corresponding instruction address is loaded.
The fork call is forwarded to the operating system and results in a new child process running the emulator. When the injected instructions execute, the child process will determine that no mask has been initialized for the address on the stack and it will generate a new one. Hence, the child process will share the same randomization key for the addresses already loaded in memory at fork time, but for the addresses it accesses later it will use it’s own key. This is problematic since the incremental attack only works if multiple attempts can be launched attacking the same key.
Perhaps an attacker could control the execution enough to ensure that the necessary masks are initialized before the child process forks to ensure they would be the same on all executions. This would only happen, however, if the server legitimately ran code on the stack before reaching the vulnerability. Hence, the RISE implementation of ISR is not vulnerable to our attack.
In order to experiment with our attack, we modified RISE to initialize the masks for all used instruction addresses before the child process forks to ensure that all child processes have the same key. Obviously, a real attacker would not have this opportunity.
In addition to the problems caused by the emulator itself, we encountered others caused by the operating system. The Fedora Linux distribution has address space layout randomization enabled by default. For our experiments, we disabled this defense. Attacks on systems using both address and instruction randomization pose additional challenges that are beyond the scope of this paper.
Table 1, Figure 8 and Figure 9 summarize the results from our experiments. The target and client ran on separate Linux dual AMD Athlon XP 2400+ machines. connected to the same network switch. For key lengths up to 128, we executed 100 trials; for longer keys, we executed 20 trials. In all cases, our attacks are nearly always able to obtain the correct key and the attack completes in under one hour, even for acquiring a 4096-byte key using the jump attack. A successful attack is an execution in which the attack client correctly guesses the desired number of key bytes. Every key byte must be correct for us to consider the attack a success.
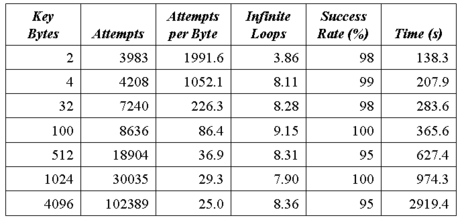 |
| Table 1. Jump attack results (averages over all trials). |
The experiments confirm the analytical predictions regarding the decrease of number of attempts per byte as key length increases. After breaking the first 12 bytes, fewer than 24 guess attempts are required per byte to acquire additional key bytes. On average, we can break a 100-byte key (enough to inject our MicroVM code) in just over six minutes with the jump attack. The return attack is faster, and requires less than two minutes. The difference is the additional approximately 4000 expected attempts the jump attack needs to guess the first two bytes simultaneously. The other difference is the increased time per attempt needed for the jump attack stemming from the infinite loops running on the server. The return attack produces an infinite loop on the server only in the unlucky circumstances when a random instruction happens to produce an infinite loop. In our experiments, the average number of infinite loops created during a return attack is 0.76. Rarely, we may be unlucky and create many infinite loops with the return attack (such as was the case for the extreme maximum time value in breaking a 4-byte key in Figure 8). The jump attack must create several infinite loops to guess the first key bytes. The actual number of loops created, shown in Table 1, varies depending on the number of apparently correct offset values.
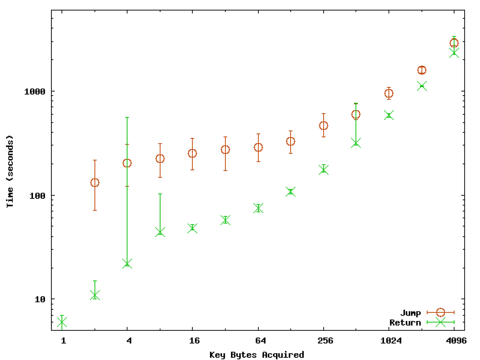 | 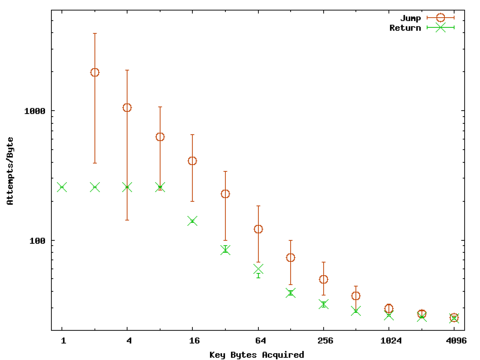 |
| Figure 8. Time to acquire key bytes. | Figure 9. Attempts per byte. |
| Times are wall-clock times measured by the client for the duration of the attack. The marked points are the median values and the bars show the 95th percentile maximum and minimum results over all trials. | |
In our initial experiments, we had surprising results where trials guessing 32-byte keys were always taking longer than guessing 2048-byte keys. The bytes placed on the stack during the near jump phase of the 32-byte attack (guessing mask bytes 5 through 11) included an 0xfe byte. This meant if the guessed instruction decrypted to a harmless instruction the execution could fall through to the 0xfe instruction and generate an infinite loop. Instead of the typical number of infinite loops, over 20 infinite loops were being created. This increased the server load enough to make the 32-byte key trials take longer than the 2048-byte keys. We modified the attack client to avoid this problem by making it select an address for starting the guessing that ensures 0xfe will not appear in the near jump offset.
In a few cases, our attack was not able to determine the correct key. The failures are caused by the inability to use certain masks because injecting the desired encrypted byte would require placing a null byte on the stack, which will cause the attack string to end before the return address is overwritten. Workarounds are possible, and necessary for the common cases. For example, in the return attack we will get an incorrect mask when a position has an apparently correct guess, but the mask is the return opcode. We assume 0xc3 is the correct mask when all the other 255 masks fail to produce the return behavior. Similarly, for the jump attack we will have false positives when the mask for the last position guessed is 0xfe. Our experimental results demonstrate that with the strategies we use the likelihood of incorrect guesses is small enough that it is not worth increasing the length and complexity of the attack code to deal with the rare special cases.
Our attack is essentially a chosen-ciphertext attack on an XOR encryption scheme. If we obtain a known ciphertext-plaintext pair with such a cipher, obtaining the encryption key is a trivial matter of XORing the plaintext and ciphertext. The challenge is obtaining a known plaintext. We do not actually obtain the plaintext for a given ciphertext guess, but instead obtain clues from the remotely observed behavior. After enough guesses, though, we can reliably determine the corresponding plaintext for an input ciphertext, and acquire the key.
This suggests some simple modifications to ISR implementations that can be used to make incremental guessing attacks much less likely to succeed. Our attack strategy would not work against any ISR scheme that uses an encryption algorithm that is not susceptible to a simple known plaintext-ciphertext attack. Any modern block encryption algorithm (such as AES [8]) satisfies this property. Unfortunately, the performance overhead of decrypting executing instructions with such an algorithm may be prohibitive. A more efficient but less secure alternative might be to randomly map each 8-bit value to a value using a lookup table. Combining this with the XOR encryption would make incremental key attacks like we propose much more difficult since it would hide the structure of the actual instruction set from the adversary.
The other property our attack relies on that is easily altered is the need to make many attempts that crash a process against a binary randomized using the same key. RISE is largely invulnerable to our attack because of the way it uses different randomization keys for forked processes. If re-randomizing is inexpensive, an implementation that re-randomizes the binary after every process or thread crash would not be susceptible to incremental key breaking attacks. This approach, however, does make the server increasingly vulnerable to denial-of-service attacks since all an attacker needs to do to force the server to shutdown and restart itself with a new randomization key is to crash a single thread.
The details of our attacks are heavily dependent on the x86 instruction set. In particular, our attacks rely on the presence of short (one or two-byte) control instructions and short harmless instructions, and benefit substantially from the structure of the conditional jump instructions. For any RISC architecture with fixed instruction length, the minimum number of key bits that must be guessed at once is determined by the instruction length. Most RISC architectures use instruction lengths of at least 32 bits, which is probably too long to realistically guess using a brute-force approach.
We have demonstrated that servers protected using ISR may be vulnerable to an incremental key-breaking attack. Our attack enables a remote attacker to acquire enough key bytes to inject an arbitrarily long worm in an ISR-protect server in approximately six minutes using the jump attack.
Our results apply only to the use of ISR at the machine instruction set level; our techniques could not be used directly to attack ISR defenses for higher-level languages such as SQL [6] and Perl [12].
Our results indicate that doing ISR in a way that provides a high degree of security against a motivated attacker is more difficult than previously thought. The most efficient ISR proposals, such as the repeated 32-bit XOR key, provide little security under realistic conditions. This does not mean ISR is no longer a promising defense strategy, but it means designers of ISR systems must consider carefully how effectively their randomization thwarts possible strategies for remotely determining the randomization key.
Acknowledgments
The authors thank Gabriela Barrantes for generously providing the RISE implementation for our experiments. We are grateful to Stephanie Forrest, Patrick Graydon, and Trent Jaeger for providing useful and insightful comments on early versions of this paper. This work benefited from fruitful discussions with Lee Badger, Steve Chapin, Jack Davidson, Dragos Halmagi, Xuxian Jiang, Angelos Keromytis, John Knight, David Mazières, Cristina Nita-Rotaru, Anh Nguyen-Tuong, Fred Schneider, Jeffrey Shirley, Mary Lou Soffa, Peter Szor, Dan Williams, Dongyan Xu, and Jinlin Yang. We thank Andrew Barrows, Jessica Greer, Scott Ruffner, and Jing Yang for technical assistance, and the Guadalajara Restaurant for Special Lunch #3. This work was supported in part by grants from the DARPA Self-Regenerative Systems Program (FA8750-04-2-0246) and the National Science Foundation (through grants NSF CAREER CCR-0092945 and NSF ITR EIA-0205327).
References
[1] Apache Software Foundation. Apache MPM Worker. Apache HTTP Server Version 2.0 Documentation. http://httpd.apache.org/docs 2.0/mod/worker.html
[2] Murat Balaban. Buffer Overflows Demystified. http://www.enderunix.org/documents/eng/bof-eng.txt
[3] Elena Gabriela Barrantes, David H. Ackley, Stephanie Forrest, Trek S. Palmer, Darko Stefanovic, and Dino Dai Zovi. Intrusion detection: Randomized instruction set emulation to disrupt binary code injection attacks. 10th ACM Conference on Computer and Communication Security (CCS), pp 281 – 289. October 2003.
[4] Elena Gabriela Barrantes, David H. Ackley, Stephanie Forrest, and Darko Stefanovic. Randomized Instruction Set Emulation. ACM Transactions on Information and System Security. In Press, 2005.
[5] Daniel Bovet and Marco Cesati. Understanding the Linux Kernel (Second Edition). O’Reilly and Associates. 2002.
[6] Stephen W. Boyd and Angelos D. Keromytis. SQLrand: Preventing SQL Injection Attacks. 2nd Applied Cryptography and Network Security Conference (ACNS). June 2004.
[7] Jedidiah R. Crandall, S. Felix Wu, and Frederic T. Chong. Experiences Using Minos as A Tool for Capturing and Analyzing Novel Worms for Unknown Vulnerabilities. GI/IEEE SIG SIDAR Conference on Detection of Intrusions and Malware and Vulnerability Assessment (DIMVA). July 2005.
[8] Joan Daemen and Vincent Rijmen. The Design of Rijndael: AES - The Advanced Encryption Standard. Springer-Verlag, 2002.
[9] Roman Danyliw. CERT Advisory CA-2003-04 MS-SQL Server Worm. January 2003.
http://www.cert.org/advisories/CS-2003-04.html
[10] eEye Digital Security. Sapphire Worm Code Disassembled. January 2003. http://www.eeye.com/html/Research/Flash/sapphire.txt
[11] Intel Corporation. Intel Architecture Software Developer’s Manual Volume 2: Instruction Set Reference. 1997. http://developer.intel.com/design/ pentium/manuals/24319101.pdf.
[12] Gaurav S. Kc, Angelos D. Keromytis, and Vassilis Prevelakis. Countering Code-Injection Attacks With Instruction-Set Randomization. 10th ACM International Conference on Computer and Communications Security (CCS). October 2003.
[13] David Litchfield. Variations in Exploit methods between Linux and Windows. July 2003. http://www.ngssoftware.com/papers/exploitvariation.pdf
[14] The NASM Project. The Netwide Assembler. http://nasm.sourceforge.net/
[15] The Pax Team. The Design and Implementation of PaX. November 2003. http://pax.grsecurity.net/docs/pax.txt
[16] Julian Seward. The Design and Implementation of Valgrind. 2003. http://developer.kde.org/~sewardj/ docs-2.0.0/mc_techdocs.html
[17] Hovav Shacham, Matthew Page, Ben Pfaff, Eu-Jin Goh, Nagendra Modadugu, Dan Boneh. On the Effectiveness of Address-Space Randomization. 11th ACM Conference on Computer and Communications Security. October 2004.
[18] Solar Designer. Return-to-libc Attack. Bugtraq Mailing List. August 1997.
A. MicroVM Code
The MicroVM code is shown below using NASM assembly code [14]. For clarity, we use symbolic constants in this code; the appropriate values would be hard coded into the injected code by the worm during deployment. NUM_BYTES is the size of the worm execution buffer (22), DATA_OFFSET is the offset from the beginning of the worm code to the beginning of the data (a four-byte value), and REG_BYTES is the number of bytes used to store the worm registers (24).
_start:
push ebp ; save frame pointer
; get location of stored worm registers
mov ebp, WORM_ADDRESS + REG_OFFSET
pop dword [ebp + DATA_OFFSET], ebp
xor eax, eax ; eax is the IP into worm
; WormIP = eax (zeroing eax starts at the beginning)
read_more_worm:
; copy next NUM_BYTES into worm execution buffer
cld
xor ecx, ecx
mov byte cl, NUM_BYTES
mov dword esi, WORM_ADDRESS
; get WormIP (points at next instruction to fetch)
add dword esi, eax
mov edi, begin_worm_exec
rep movsb
; change next WormIP to point to next block
add eax, NUM_BYTES
pushad ; save MicroVM registers
; load worm registers
mov edi, dword [ebp + EDI_OFFSET]
… ; do the same for esi, eax, ebx, ecx, and edx
begin_worm_exec:
nop ; Reserve NUM_BYTES using nops to leave
nop ; room for worm code fragment
… ; end of worm code space
; save worm registers
mov [ebp + EDI_OFFSET],edi
… ; do the same for esi, eax, ebx, ecx, and edx
popad ; load MicroVM registers
jmp read_more_worm