CS302 -- Project 5 -- Letter Dice
- CS302 -- Advanced Data Structures and Algorithms
- Spring, 2020
- Courtesy of James S. Plank
- Original file:
http://web.eecs.utk.edu/~jplank/plank/classes/cs302/Labs/Lab9
A prior 302/307 TA Camille Crumpton (2017) posted youtube videos to help with this project -- they are here.
Introduction
NOTE: We recommend that you work with a single partner on this project. You also may work alone.
Suppose you are given some number of "word dice", as in the picture below:
 |
We won't constrain dice to have six sides -- we'll assume that a die may have any number
of sides, and that the length of and an input string itself defines the number of sides and possible letters, respectively, of
a corresponding die.
For example, let's assume that the above dice only have three sides each -- the sides that you can see. Then, the file Dice1.txt defines the four dice pictured:
ENG SAA PRR EAE |
The problem you must solve
Your task is to write a program called worddice. The input to this program is as follows:- The dice available, encoded as described above.
- A list words to check if they can be spelled using these dice
However, you cannot spell "PEEN", even though all the letters are there, because you would have to use the "ENG" die for both the 'E' and 'N'.
Input/output
The dice described above must be present in an input file. Each die may have any number of letters, and, within a file, the dice may all have differing numbers of letters. The word list is simply a second file containing words, one per line.For each word in the word list, your program should print out one of the following:
- If the word cannot be spelled: "Cannot spell word".
- If the word can be spelled: The order of the dice used to spell out the word, then the word. The dice are numbered starting with zero.
UNIX> cat Dice1.txt ENG SAA PRR EAE UNIX> cat Words1.txt RAGE SEEP PEEN GASP UNIX> worddice Dice1.txt Words1.txt 2,1,0,3: RAGE 1,0,3,2: SEEP Cannot spell PEEN 0,3,1,2: GASP UNIX>
Organizing the program
This is an example of a bipartite matching. For each word, set up a graph that matches dice to letters of the words. For example, here are the above dice with the word "RAGE":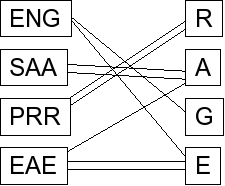 |
Dr. Plank has included double-edges for the duplicate letters. Your program can eliminate these if you
want, since duplicate letters don't help you at all and just make your program run slower. We'll accept either way.
You want to find a matching of this graph that is composed of edges that connect two nodes, where no edge is incident to the same node.
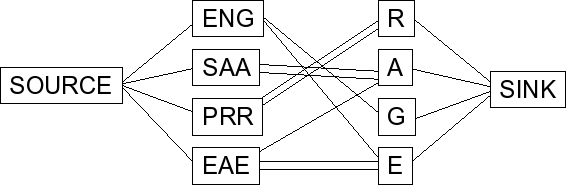
To do this, you convert the graph into one in which network flow will solve the problem: a source node connected to each die, and a sink node connected to each letter of the word:
 |
Finding the maximum flow will discover the matching if it exists. Here is
the flow/matching in this example:
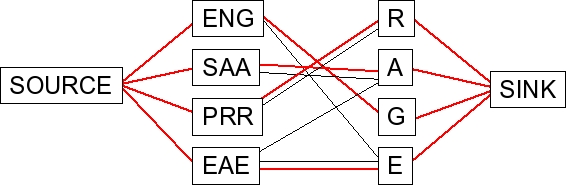 |
Your program should use the Edmonds-Karp algorithm to determine maximum flow. The fact that
all edges have weight one makes this easier.
Dr. Plank's implementation is slow for two reasons. First, he creates and destroys the graph with each word. It would be faster if he never deleted the source and dice nodes/edges. Second, when he created the edges to each letter of the word, he used the Find() method on the dice strings. That is inefficient as compared with other potential optimizations, but probably what you will also use given what we have covered in 140/302.
Hint: read the input and create the graphs first
The program readorig was the first step for both of us -- reading the input, creating the network flow graph, and printing it out. Note, in sample output below from Dr. Plank, his program does not have duplicate edges. This will help get you started.UNIX> readorig Dice1.txt Words1.txt Node 0: SOURCE Edges to 1 2 3 4 Node 1: ENG Edges to 7 8 Node 2: SAA Edges to 6 Node 3: PRR Edges to 5 Node 4: EAE Edges to 6 8 Node 5: R Edges to 9 Node 6: A Edges to 9 Node 7: G Edges to 9 Node 8: E Edges to 9 Node 9: SINK Edges to Node 0: SOURCE Edges to 1 2 3 4 Node 1: ENG Edges to 6 7 Node 2: SAA Edges to 5 Node 3: PRR Edges to 8 Node 4: EAE Edges to 6 7 Node 5: S Edges to 9 Node 6: E Edges to 9 Node 7: E Edges to 9 Node 8: P Edges to 9 Node 9: SINK Edges to Node 0: SOURCE Edges to 1 2 3 4 Node 1: ENG Edges to 6 7 8 Node 2: SAA Edges to Node 3: PRR Edges to 5 Node 4: EAE Edges to 6 7 Node 5: P Edges to 9 Node 6: E Edges to 9 Node 7: E Edges to 9 Node 8: N Edges to 9 Node 9: SINK Edges to Node 0: SOURCE Edges to 1 2 3 4 Node 1: ENG Edges to 5 Node 2: SAA Edges to 6 7 Node 3: PRR Edges to 8 Node 4: EAE Edges to 6 Node 5: G Edges to 9 Node 6: A Edges to 9 Node 7: S Edges to 9 Node 8: P Edges to 9 Node 9: SINK Edges to UNIX>
Examples
Dr. Plank has provided a few additional example files:Dice2.txt and Words2.txt are small files to test variable-sized dice:
UNIX> cat Dice2.txt E PITED FOGCEF UNIX> cat Words2.txt DOG PIG CAT DO TEE FEE UNIX> worddice Dice2.txt Words2.txt Cannot spell DOG Cannot spell PIG Cannot spell CAT 1,2: DO 1,0,2: TEE 2,0,1: FEE UNIX>
Dice3.txt is a file with six randomly generated six-sided dice, and Words3.txt contains all words from the Unix dictionary that have six letters.
UNIX> cat Dice3.txt IBTLCP DUAQEM DXLOTN WMIVQA NDCLOT JKCEMR UNIX> head Words3.txt AARHUS ABACUS ABATER ABBOTT ABDUCT ABJECT ABLATE ABLAZE ABOARD ABOUND UNIX> worddice Dice3.txt Words3.txt | head Cannot spell AARHUS Cannot spell ABACUS Cannot spell ABATER Cannot spell ABBOTT 3,0,2,1,5,4: ABDUCT 3,0,5,1,4,2: ABJECT 1,0,2,3,4,5: ABLATE Cannot spell ABLAZE 1,0,2,3,5,4: ABOARD Cannot spell ABOUND UNIX>
Dice4.txt is a file with eight randomly generated dice with between three and seven sides. Words4.txt contains all words from the Unix dictionary that have eight letters. As worddice shows, there are fewer successful spellings in this example:
UNIX> cat Dice4.txt FJZ BSYQ WYUTI SHTXVU PRAFYBH LWQCEI ENLJB BTJO UNIX> head Words4.txt ABDICATE ABERDEEN ABERRANT ABERRATE ABETTING ABEYANCE ABHORRED ABLUTION ABNORMAL ABORNING UNIX> worddice Dice4.txt Words4.txt | head Cannot spell ABDICATE Cannot spell ABERDEEN Cannot spell ABERRANT Cannot spell ABERRATE Cannot spell ABETTING Cannot spell ABEYANCE Cannot spell ABHORRED Cannot spell ABLUTION Cannot spell ABNORMAL Cannot spell ABORNING UNIX> worddice Dice4.txt Words4.txt | grep ':' | head 7,6,4,2,3,5,0,1: BEAUTIFY 1,6,7,2,0,5,3,4: BLOWFISH 7,5,3,6,0,2,1,4: BLUEFISH 6,7,4,1,2,0,3,5: BOASTFUL 5,0,4,3,1,2,7,6: EFFUSION 0,4,6,2,5,7,3,1: FABULOUS 0,6,4,7,5,2,3,1: FEROCITY 0,5,1,7,2,3,4,6: FESTIVAL 0,2,6,4,7,3,5,1: FIBROSIS 0,6,4,2,3,5,1,7: FLAUTIST UNIX>
The Gradescript
There will be a program called grader in the lab directory which is used to determine if your output is correct via matching ours.
Additional requirements
When you are finished implementing your worddice implementation, each member must provide a brief summary
of their individual contributions to the project and answer the following question:
-
What is complexity of your implementation?
Explain this by describing which data structures you used and how you used them to implement network flow.
Submission instructions
Please have one team member submit an archive of the following files (not in a subdirectory of the archive) on Canvas to aid us in grading:
- source files for worddice
- Text document summarizing the student who is uploading's contributions and their answers to the required question
- Makefile (even if you use the provided Makefile, please include it)
If you work in a pair, the team member who isnít submitting the above files should write up a separate document with their contributions and answer and submit only that on Canvas.
Rubric
Your project will be scored as follows:
+2 Code is well formatted, commented (inc. name, assignment, and overview), with reasonable variable names +55 55 points * % of gradescripts passed +3 Responses, inc. individual contributions