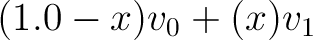Cubic Splines
Cubic Splines take a 4-vector called an disjoint sub-interval [where the interval point (usually designated as t or x) varies from 0.0 to 1.0], multiply that with a 4x4 spline matrix, and finally multiply that with a 4x1 matrix of the control points (click a specific spline to see what this looks like).
To create a spline, apply the designated transformation to both the X and the Y coordinate.
For Example: A linear transformation would be (remember lowercase x is the interval point between 0.0 to 1.0):
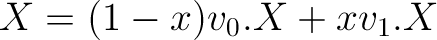
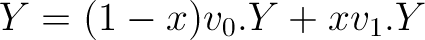
(C++) codewise:
vector<Point> generateLinearPoints(Point &v0, Point &v1) {
vector<Point> splinePoints;
for (float x = 0.0f;x <= 1.0f;x += 0.01f) {
float spXCoordinate = ((1.0f - x) * v0.X) + x * v1.X;
float spYCoordinate = ((1.0f - x) * v0.Y) + x * v1.Y;
splinePoints.push_back(Point(spXCoordinate, spYCoordinate));
}
return splinePoints;
}
Now the vector splinePoints contains 100 (0.0 to 1.0 at a 0.01 increment) X,Y coordinates for the interpolation between control points v0 and v1.
The smaller the increment (0.01 seems to work well for relatively close control points) the more discrete points, and the interpolated spline will be "thicker" because the interpolated points will be closer together.
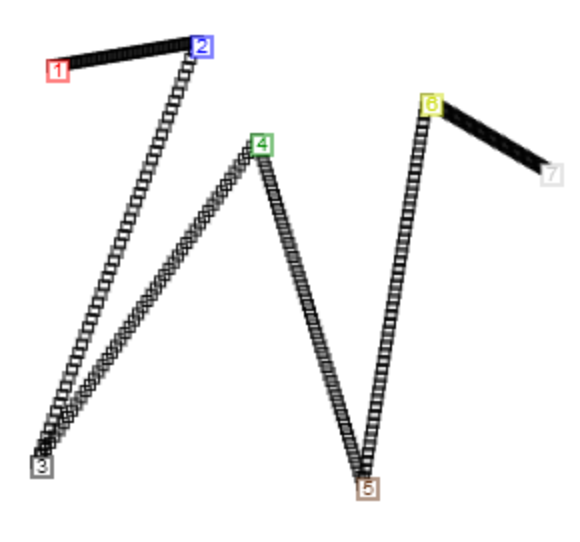
Click on a spline on the left (or click "Web Splines" to do it yourself) to see how the splines work. Each black square is in a vector like splinePoints.
Catmull-Rom
The Catmull-Rom spline has the following properties:
Curve starts at second control point and ends at the third
C(0) and C(1) continuity
Does NOT satisfy convex-hull property
Curves pass through all control points (except the first and last)
The matrix form for a Catmull-Rom curve using four control points v0, v1, v2, v3, and interval point x is:
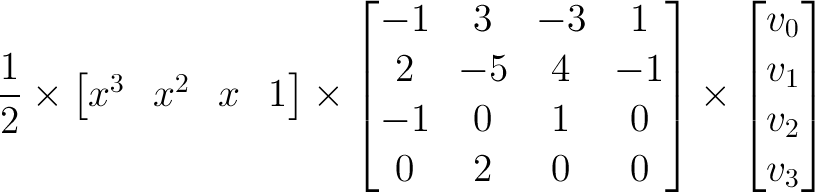
Equation form (apply this equation to the x coordinates of v0, v1, v2, v3, and then do the same for the y coordinates):
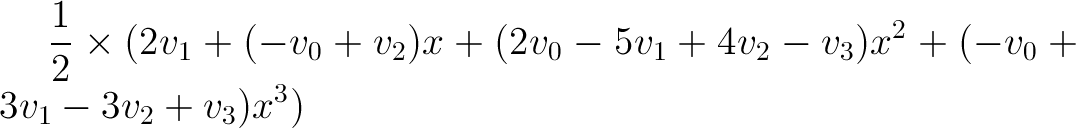
Example of a Catmull-Rom Curve:
Uniform Basis (B-Spline)
The Basis (or B) spline has the following properties:
C(0), C(1), and C(2) continuity
Curve may not go through ANY control points (very hard to precisely target)
Satisfies the convex-hull property
The smoothest curve out of Catmull-Rom and Bezier
The matrix form for a Basis curve using four control points v0, v1, v2, v3, and interval point x is:
Equation form (apply this equation to the x coordinates of v0, v1, v2, v3, and then do the same for the y coordinates):
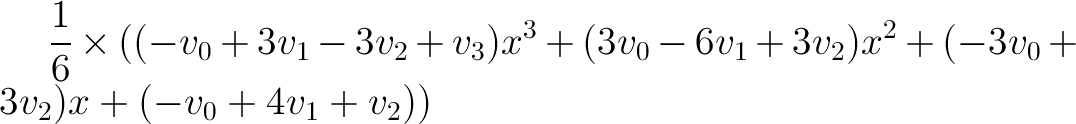
Bezier
The Bezier spline has the following properties:
C(0) and C(1) continuity
Smoothness at join points are made by making the adjacent points colinear
Obeys convex hull property
Spline goes through two endpoints
The matrix form for a Bezier curve using four control points v0, v1, v2, v3, and interval point x is:
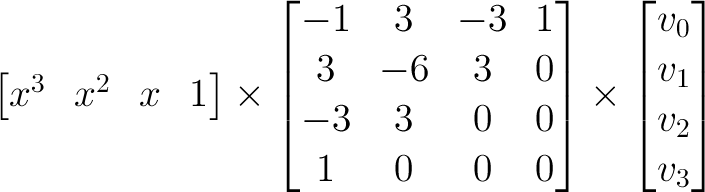
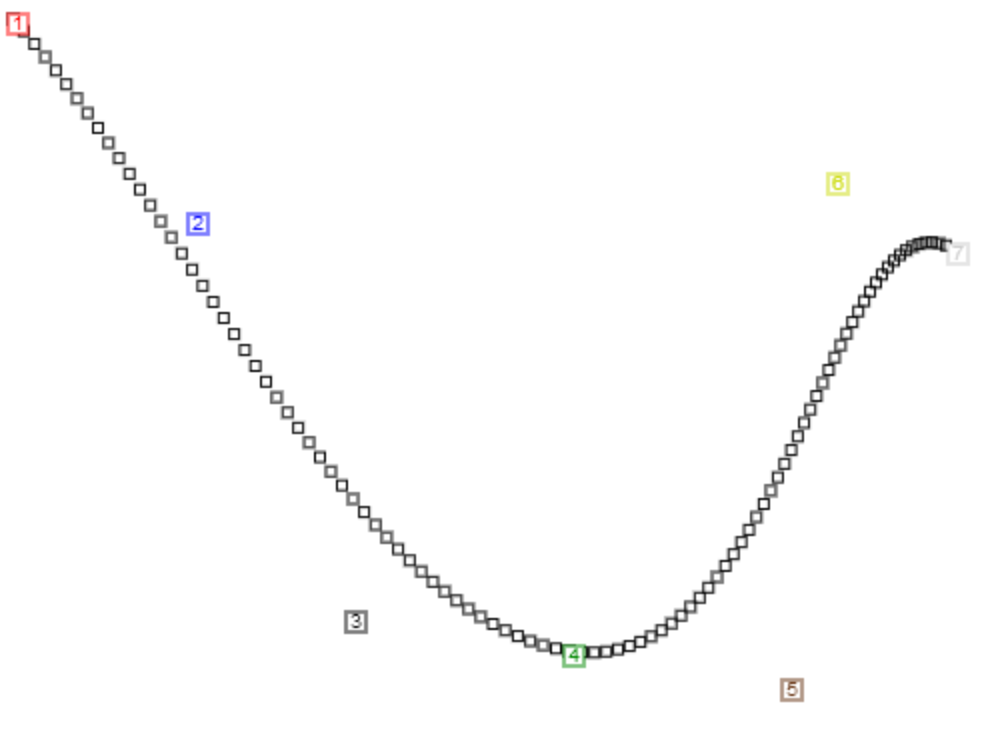
Equation form (apply this equation to the x coordinates of v0, v1, v2, v3, and then do the same for the y coordinates):
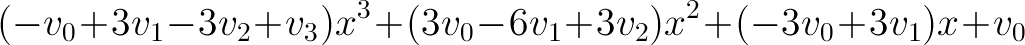
Bezier Curve Without Colinearity (notice the abruptness at join point 4)
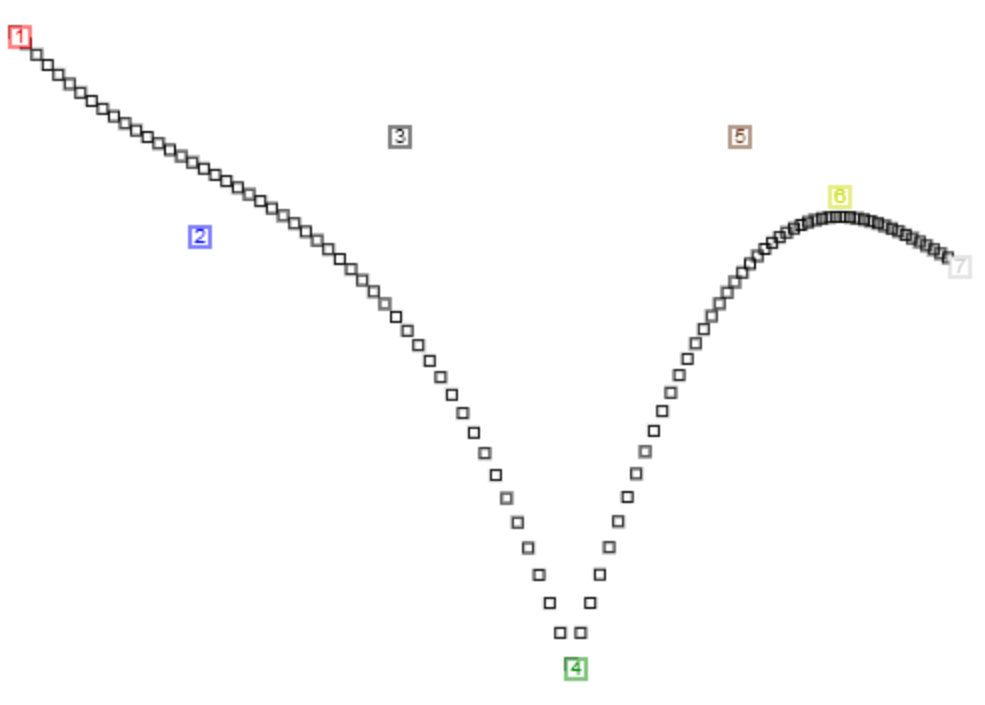
Bezier Curve With Colinearity (notice the smoothness at join point 4 and co-points 3 and 5 are in a line through point 4)
To modify the points to enforce colinearity, apply this equation (updates point 5 based on the user moving point 3 and pivoting around point 4):
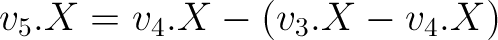
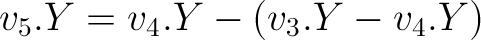
Linear Interpolation
While linear interpolation is not a cubic spline, it is good to demonstrate how the disjoint sub-interval works.
A linear interpolation between two control points v0 and v1 and interval point x:
