The algorithm for computing the GUPTRI form is based on two reductions
(staircase forms) [121].
The first is the ![]() -staircase form that reveals
the right singular structure and the Jordan structure of
the zero eigenvalue of
-staircase form that reveals
the right singular structure and the Jordan structure of
the zero eigenvalue of ![]() .
.
The ![]() -algorithm uses a finite number of unitary equivalence
transformations, where in
step
-algorithm uses a finite number of unitary equivalence
transformations, where in
step
![]() ,
, ![]() dimension of the
column null space of
dimension of the
column null space of ![]() and
and
![]() dimension of the intersecting column null space of
dimension of the intersecting column null space of ![]() and
and
![]() are determined.
Here,
are determined.
Here, ![]() and
and ![]() , and
, and
![]() for
for ![]() correspond to the deflated matrix pair obtained after
the equivalence transformation in step
correspond to the deflated matrix pair obtained after
the equivalence transformation in step ![]() .
The structure indices (
.
The structure indices (![]() -indices) display the Kronecker structure as follows:
-indices) display the Kronecker structure as follows:
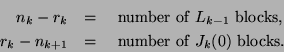
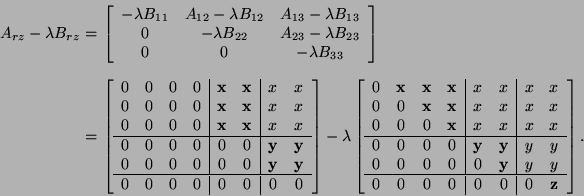
Nonzero entries after each deflation are marked with
a unique letter (x from first step, y from second step, etc.),
and they appear in bold or italic.
The superdiagonal blocks of ![]() have full column rank and
the diagonal blocks of
have full column rank and
the diagonal blocks of ![]() have full row rank.
The nonzero entries of the full rank blocks are marked in
bold font.
We use this notation in later examples as well.
have full row rank.
The nonzero entries of the full rank blocks are marked in
bold font.
We use this notation in later examples as well.
The diagonal blocks (defining the ``stairs'') in
![]() are of size
are of size
![]() and show the following information:
and show the following information:
![\begin{eqnarray*}
&&\!\!\! n_1 = 4 = {\rm dim}~{\cal N}(A^{(1)}), \quad
r_1 = 3 ...
...{(3)}),
\\ [2mm] &&\!\!\!
n_4 = 0 = {\rm dim}~{\cal N}(A^{(4)}).
\end{eqnarray*}](img3156.png)
In general, let ![]() and
and ![]() be complex
be complex ![]() matrices.
Then it can be shown that there exist unitary matrices
matrices.
Then it can be shown that there exist unitary matrices
![]() and
and
![]() such that
the matrix pencil
such that
the matrix pencil ![]() is transformed to
the following so-called
RZ-staircase form [121,122]:
U^*(A - B)V =
[
is transformed to
the following so-called
RZ-staircase form [121,122]:
U^*(A - B)V =
[
![]()
] -
[
![]()
],
where the staircase block structure of ![]() and
and ![]() reveals the
right singular structure and the Jordan structure of
the zero eigenvalue of
reveals the
right singular structure and the Jordan structure of
the zero eigenvalue of ![]() :
:
![\begin{array}{c}
A_{rz}=
\left[
\begin{array}{cccccc}
0 & A_{12} & * & * & * & ...
...0 & \cdots & 0 & 0 & B_{j-1,j-1} & B_{j-1,j} \\
\end{array}\right].
\end{array}](img3162.png)
The subblocks in (8.37) and (8.38)
have the following properties:
Three cases can appear in the ![]() -staircase form depending on
-staircase form depending on
![]() and
and ![]() :
:
We see that the ![]() example above corresponds to case 3 and
that
example above corresponds to case 3 and
that
![]() does not have a
does not have a ![]() th block column.
th block column.
The second reduction is the ![]() (left-infinity)-staircase form
that reveals the left singular structure and the Jordan structure of
the infinite eigenvalue of
(left-infinity)-staircase form
that reveals the left singular structure and the Jordan structure of
the infinite eigenvalue of ![]() .
This dual staircase form is obtained by working from the southeast
corner of
.
This dual staircase form is obtained by working from the southeast
corner of ![]() and replacing column compressions by row compressions
in the
and replacing column compressions by row compressions
in the ![]() -algorithm.
The block indices
-algorithm.
The block indices ![]() and
and ![]() are dimensions of corresponding
row null spaces and define the
are dimensions of corresponding
row null spaces and define the ![]() -indices.
Moreover,
-indices.
Moreover, ![]() and
and ![]() are the
number of
are the
number of ![]() and
and ![]() blocks, respectively.
blocks, respectively.
Both the ![]() -staircase and
-staircase and ![]() -staircase reductions give us two types of
structure elements which must be separated to
obtain the GUPTRI form.
For example, the right singular structure and the Jordan
structure of the zero eigenvalue are separated by first applying the
-staircase reductions give us two types of
structure elements which must be separated to
obtain the GUPTRI form.
For example, the right singular structure and the Jordan
structure of the zero eigenvalue are separated by first applying the
![]() -staircase reduction to
-staircase reduction to
![]() and insisting on the same
right minimal indices.
Then we obtain
and insisting on the same
right minimal indices.
Then we obtain ![]() and are left with a pencil,
say,
and are left with a pencil,
say,
![]() corresponding to the zero eigenvalue.
Finally,
corresponding to the zero eigenvalue.
Finally, ![]() is obtained by transforming
is obtained by transforming
![]() to
to ![]() -staircase form.
-staircase form.
We return to the ![]() example and show the separated
example and show the separated
![]() -staircase and
-staircase and ![]() -staircase forms:
-staircase forms:
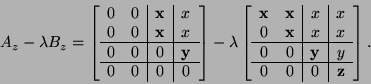
|
|
|
In summary, the GUPTRI algorithm for computing
(8.34) and (8.35) comprises
seven reduction steps.
The first three steps apply the ![]() -staircase reduction to
different blocks of
-staircase reduction to
different blocks of ![]() , giving the right singular structure
(
, giving the right singular structure
(
![]() ) and the zero Jordan structure (
) and the zero Jordan structure (
![]() )
in the top left corner of
)
in the top left corner of ![]() and
and ![]() .
Similarly, the next three steps apply the
.
Similarly, the next three steps apply the ![]() -staircase reduction
to different blocks of the remaining pencil, giving the infinite Jordan
structure (
-staircase reduction
to different blocks of the remaining pencil, giving the infinite Jordan
structure (
![]() ) and the left singular structure
(
) and the left singular structure
(
![]() ) in the bottom right corner of
) in the bottom right corner of ![]() and
and ![]() .
Then a square regular pencil is left in the middle of the
transformed pencil, which corresponds to the finite and nonzero
eigenvalues of
.
Then a square regular pencil is left in the middle of the
transformed pencil, which corresponds to the finite and nonzero
eigenvalues of ![]() .
By applying the QZ algorithm to this pencil,
the upper triangular block
.
By applying the QZ algorithm to this pencil,
the upper triangular block
![]() is obtained.
is obtained.