Chapter 13

Objects of Vectors

13.1 Enumerated types

In the previous chapter I talked about mappings between real-world values like rank and suit, and internal representations like integers and strings. Although we created a mapping between ranks and integers, and between suits and integers, I pointed out that the mapping itself does not appear as part of the program.

Actually, C++ provides a feature called and enumerated type that makes it possible to (1) include a mapping as part of the program, and (2) define the set of values that make up the mapping. For example, here is the definition of the enumerated types Suit and Rank:

enum Suit { CLUBS, DIAMONDS, HEARTS, SPADES };

enum Rank { ACE=1, TWO, THREE, FOUR, FIVE, SIX, SEVEN, EIGHT, NINE,
TEN, JACK, QUEEN, KING };

By default, the first value in the enumerated type maps to 0, the second to 1, and so on. Within the Suit type, the value CLUBS is represented by the integer 0, DIAMONDS is represented by 1, etc.

The definition of Rank overrides the default mapping and specifies that ACE should be represented by the integer 1. The other values follow in the usual way.

Once we have defined these types, we can use them anywhere. For example, the instance variables rank and suit are can be declared with type Rank and Suit:

struct Card
{
Rank rank;
Suit suit;

Card (Suit s, Rank r);
};

That the types of the parameters for the constructor have changed, too. Now, to create a card, we can use the values from the enumerated type as arguments:

Card card (DIAMONDS, JACK);

By convention, the values in enumerated types have names with all capital letters. This code is much clearer than the alternative using integers:

Card card (1, 11);

Because we know that the values in the enumerated types are represented as integers, we can use them as indices for a vector. Therefore the old print function will work without modification. We have to make some changes in buildDeck, though:

int index = 0;
for (Suit suit = CLUBS; suit <= SPADES; suit = Suit(suit+1)) {
for (Rank rank = ACE; rank <= KING; rank = Rank(rank+1)) {
deck[index].suit = suit;
deck[index].rank = rank;
index++;
}
}

In some ways, using enumerated types makes this code more readable, but there is one complication. Strictly speaking, we are not allowed to do arithmetic with enumerated types, so suit++ is not legal. On the other hand, in the expression suit+1, C++ automatically converts the enumerated type to integer. Then we can take the result and typecast it back to the enumerated type:

suit = Suit(suit+1);
rank = Rank(rank+1);

Actually, there is a better way to do this—we can define the ++ operator for enumerated types—but that is beyond the scope of this book.

13.2 switch statement

It's hard to mention enumerated types without mentioning switch statements, because they often go hand in hand. A switch statement is an alternative to a chained conditional that is syntactically prettier and often more efficient. It looks like this:

switch (symbol) {
case '+':
perform_addition ();
break;
case '*':
perform_multiplication ();
break;
default:
cout << "I only know how to perform addition and multiplication" << endl;
break;
}

This switch statement is equivalent to the following chained conditional:

if (symbol == '+') {
perform_addition ();
} else if (symbol == '*') {
perform_multiplication ();
} else {
cout << "I only know how to perform addition and multiplication" << endl;
}

The break statements are necessary in each branch in a switch statement because otherwise the flow of execution "falls through" to the next case. Without the break statements, the symbol + would make the program perform addition, and then perform multiplication, and then print the error message. Occasionally this feature is useful, but most of the time it is a source of errors when people forget the break statements.

switch statements work with integers, characters, and enumerated types. For example, to convert a Suit to the corresponding string, we could use something like:

switch (suit) {
case CLUBS: return "Clubs";
case DIAMONDS: return "Diamonds";
case HEARTS: return "Hearts";
case SPADES: return "Spades";
default: return "Not a valid suit";
}

In this case we don't need break statements because the return statements cause the flow of execution to return to the caller instead of falling through to the next case.

In general it is good style to include a default case in every switch statement, to handle errors or unexpected values.

13.3 Decks

In the previous chapter, we worked with a vector of objects, but I also mentioned that it is possible to have an object that contains a vector as an instance variable. In this chapter I am going to create a new object, called a Deck, that contains a vector of Cards.

The structure definition looks like this

struct Deck {
vector<Card> cards;

Deck (int n);
};

Deck::Deck (int size)
{
vector<Card> temp (size);
cards = temp;
}

The name of the instance variable is cards to help distinguish the Deck object from the vector of Cards that it contains.

For now there is only one constructor. It creates a local variable named temp, which it initializes by invoking the constructor for the vector class, passing the size as a parameter. Then it copies the vector from temp into the instance variable cards.

Now we can create a deck of cards like this:

Deck deck (52);

Here is a state diagram showing what a Deck object looks like:

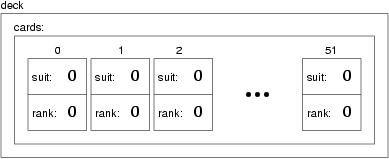
The object named deck has a single instance variable named cards, which is a vector of Card objects. To access the cards in a deck we have to compose the syntax for accessing an instance variable and the syntax for selecting an element from an array. For example, the expression deck.cards[i] is the ith card in the deck, and deck.cards[i].suit is its suit. The following loop

for (int i = 0; i<52; i++) {
deck.cards[i].print();
}

demonstrates how to traverse the deck and output each card.

13.4 Another constructor

Now that we have a Deck object, it would be useful to initialize the cards in it. From the previous chapter we have a function called buildDeck that we could use (with a few adaptations), but it might be more natural to write a second Deck constructor.

Deck::Deck ()
{
vector<Card> temp (52);
cards = temp;

int i = 0;
for (Suit suit = CLUBS; suit <= SPADES; suit = Suit(suit+1)) {
for (Rank rank = ACE; rank <= KING; rank = Rank(rank+1)) {
cards[i].suit = suit;
cards[i].rank = rank;
i++;
}
}
}

Notice how similar this function is to buildDeck, except that we had to change the syntax to make it a constructor. Now we can create a standard 52-card deck with the simple declaration Deck deck;

13.5 Deck member functions

Now that we have a Deck object, it makes sense to put all the functions that pertain to Decks in the Deck structure definition. Looking at the functions we have written so far, one obvious candidate is printDeck (Section 12.7). Here's how it looks, rewritten as a Deck member function:

void Deck::print () const {
for (int i = 0; i < cards.size(); i++) {
cards[i].print ();
}
}

As usual, we can refer to the instance variables of the current object without using dot notation.

For some of the other functions, it is not obvious whether they should be member functions of Card, member functions of Deck, or nonmember functions that take Cards and Decks as parameters. For example, the version of find in the previous chapter takes a Card and a Deck as arguments, but you could reasonably make it a member function of either type. As an exercise, rewrite find as a Deck member function that takes a Card as a parameter.

Writing find as a Card member function is a little tricky. Here's my version:

int Card::find (const Deck& deck) const {
for (int i = 0; i < deck.cards.size(); i++) {
if (equals (deck.cards[i], *this)) return i;
}
return -1;
}

The first trick is that we have to use the keyword this to refer to the Card the function is invoked on.

The second trick is that C++ does not make it easy to write structure definitions that refer to each other. The problem is that when the compiler is reading the first structure definition, it doesn't know about the second one yet.

One solution is to declare Deck before Card and then define Deck afterwards:

// declare that Deck is a structure, without defining it
struct Deck;

// that way we can refer to it in the definition of Card
struct Card
{
int suit, rank;

Card ();
Card (int s, int r);

void print () const;
bool isGreater (const Card& c2) const;
int find (const Deck& deck) const;
};

// and then later we provide the definition of Deck
struct Deck {
vector<Card> cards;

Deck ();
Deck (int n);
void print () const;
int find (const Card& card) const;
};

13.6 Shuffling

For most card games you need to be able to shuffle the deck; that is, put the cards in a random order. In Section 10.5 we saw how to generate random numbers, but it is not obvious how to use them to shuffle a deck.

One possibility is to model the way humans shuffle, which is usually by dividing the deck in two and then reassembling the deck by choosing alternately from each deck. Since humans usually don't shuffle perfectly, after about 7 iterations the order of the deck is pretty well randomized. But a computer program would have the annoying property of doing a perfect shuffle every time, which is not really very random. In fact, after 8 perfect shuffles, you would find the deck back in the same order you started in. For a discussion of that claim, see http://www.wiskit.com/marilyn/craig.html or do a web search with the keywords "perfect shuffle."

A better shuffling algorithm is to traverse the deck one card at a time, and at each iteration choose two cards and swap them.

Here is an outline of how this algorithm works. To sketch the program, I am using a combination of C++ statements and English words that is sometimes called pseudocode:

for (int i=0; i<cards.size(); i++) {
// choose a random number between i and cards.size()
// swap the ith card and the randomly-chosen card
}

The nice thing about using pseudocode is that it often makes it clear what functions you are going to need. In this case, we need something like randomInt, which chooses a random integer between the parameters low and high, and swapCards which takes two indices and switches the cards at the indicated positions.

You can probably figure out how to write randomInt by looking at Section 10.5, although you will have to be careful about possibly generating indices that are out of range.

You can also figure out swapCards yourself. I will leave the remaining implementation of these functions as an exercise to the reader.

13.7 Sorting

Now that we have messed up the deck, we need a way to put it back in order. Ironically, there is an algorithm for sorting that is very similar to the algorithm for shuffling.

Again, we are going to traverse the deck and at each location choose another card and swap. The only difference is that this time instead of choosing the other card at random, we are going to find the lowest card remaining in the deck.

By "remaining in the deck," I mean cards that are at or to the right of the index i.

for (int i=0; i<cards.size(); i++) {
// find the lowest card at or to the right of i
// swap the ith card and the lowest card
}

Again, the pseudocode helps with the design of the helper functions. In this case we can use swapCards again, so we only need one new one, called findLowestCard, that takes a vector of cards and an index where it should start looking.

This process, using pseudocode to figure out what helper functions are needed, is sometimes called top-down design, in contrast to the bottom-up design I discussed in Section 10.8.

Once again, I am going to leave the implementation up to the reader.

13.8 Subdecks

How should we represent a hand or some other subset of a full deck? One easy choice is to make a Deck object that has fewer than 52 cards.

We might want a function, subdeck, that takes a vector of cards and a range of indices, and that returns a new vector of cards that contains the specified subset of the deck:

Deck Deck::subdeck (int low, int high) const {
Deck sub (high-low+1);

for (int i = 0; i<sub.cards.size(); i++) {
sub.cards[i] = cards[low+i];
}
return sub;
}

To create the local variable named subdeck we are using the Deck constructor that takes the size of the deck as an argument and that does not initialize the cards. The cards get initialized when they are copied from the original deck.

The length of the subdeck is high-low+1 because both the low card and high card are included. This sort of computation can be confusing, and lead to "off-by-one" errors. Drawing a picture is usually the best way to avoid them.

As an exercise, write a version of findBisect that takes a subdeck as an argument, rather than a deck and an index range. Which version is more error-prone? Which version do you think is more efficient?

13.9 Shuffling and dealing

In Section 13.6 I wrote pseudocode for a shuffling algorithm. Assuming that we have a function called shuffleDeck that takes a deck as an argument and shuffles it, we can create and shuffle a deck:

Deck deck; // create a standard 52-card deck
deck.shuffle (); // shuffle it

Then, to deal out several hands, we can use subdeck:

Deck hand1 = deck.subdeck (0, 4);
Deck hand2 = deck.subdeck (5, 9);
Deck pack = deck.subdeck (10, 51);

This code puts the first 5 cards in one hand, the next 5 cards in the other, and the rest into the pack.

When you thought about dealing, did you think we should give out one card at a time to each player in the round-robin style that is common in real card games? I thought about it, but then realized that it is unnecessary for a computer program. The round-robin convention is intended to mitigate imperfect shuffling and make it more difficult for the dealer to cheat. Neither of these is an issue for a computer.

This example is a useful reminder of one of the dangers of engineering metaphors: sometimes we impose restrictions on computers that are unnecessary, or expect capabilities that are lacking, because we unthinkingly extend a metaphor past its breaking point. Beware of misleading analogies.

13.10 Mergesort

In Section 13.7, we saw a simple sorting algorithm that turns out not to be very efficient. In order to sort n items, it has to traverse the vector n times, and each traversal takes an amount of time that is proportional to n. The total time, therefore, is proportional to n².

In this section I will sketch a more efficient algorithm called mergesort. To sort n items, mergesort takes time proportional to n log n. That may not seem impressive, but as n gets big, the difference between n² and n log n can be enormous. Try out a few values of n and see.

The basic idea behind mergesort is this: if you have two subdecks, each of which has been sorted, it is easy (and fast) to merge them into a single, sorted deck. Try this out with a deck of cards:

Form two subdecks with about 10 cards each and sort them so that when they are face up the lowest cards are on top. Place both decks face up in front of you.
Compare the top card from each deck and choose the lower one. Flip it over and add it to the merged deck.
Repeat step two until one of the decks is empty. Then take the remaining cards and add them to the merged deck.

The result should be a single sorted deck. Here's what this looks like in pseudocode:

Deck merge (const Deck& d1, const Deck& d2) {
// create a new deck big enough for all the cards
Deck result (d1.cards.size() + d2.cards.size());

// use the index i to keep track of where we are in
// the first deck, and the index j for the second deck
int i = 0;
int j = 0;

// the index k traverses the result deck
for (int k = 0; k<result.cards.size(); k++) {

// if d1 is empty, d2 wins; if d2 is empty, d1 wins;
// otherwise, compare the two cards

// add the winner to the new deck
}
return result;
}

I chose to make merge a nonmember function because the two arguments are symmetric.

The best way to test merge is to build and shuffle a deck, use subdeck to form two (small) hands, and then use the sort routine from the previous chapter to sort the two halves. Then you can pass the two halves to merge to see if it works.

If you can get that working, try a simple implementation of mergeSort:

Deck Deck::mergeSort () const {
// find the midpoint of the deck
// divide the deck into two subdecks
// sort the subdecks using sort
// merge the two halves and return the result
}

Notice that the current object is declared const because mergeSort does not modify it. Instead, it creates and returns a new Deck object.

If you get that version working, the real fun begins! The magical thing about mergesort is that it is recursive. At the point where you sort the subdecks, why should you invoke the old, slow version of sort? Why not invoke the spiffy new mergeSort you are in the process of writing?

Not only is that a good idea, it is necessary in order to achieve the performance advantage I promised. In order to make it work, though, you have to add a base case so that it doesn't recurse forever. A simple base case is a subdeck with 0 or 1 cards. If mergesort receives such a small subdeck, it can return it unmodified, since it is already sorted.

The recursive version of mergesort should look something like this:

Deck Deck::mergeSort (Deck deck) const {
// if the deck is 0 or 1 cards, return it

// find the midpoint of the deck
// divide the deck into two subdecks
// sort the subdecks using mergesort
// merge the two halves and return the result
}

As usual, there are two ways to think about recursive programs: you can think through the entire flow of execution, or you can make the "leap of faith." I have deliberately constructed this example to encourage you to make the leap of faith.

When you were using sort to sort the subdecks, you didn't feel compelled to follow the flow of execution, right? You just assumed that the sort function would work because you already debugged it. Well, all you did to make mergeSort recursive was replace one sort algorithm with another. There is no reason to read the program differently.

Well, actually you have to give some thought to getting the base case right and making sure that you reach it eventually, but other than that, writing the recursive version should be no problem. Good luck!

13.11 Glossary

pseudocode: A way of designing programs by writing rough drafts in a combination of English and C++.
helper function: Often a small function that does not do anything enormously useful by itself, but which helps another, more useful, function.
bottom-up design: A method of program development that uses pseudocode to sketch solutions to large problems and design the interfaces of helper functions.
mergesort: An algorithm for sorting a collection of values. Mergesort is faster than the simple algorithm in the previous chapter, especially for large collections.

Revised 2008-12-06.